Trong không gian với hệ tọa độ $Oxyz$, cho mặt cầu \((S)\) : \({(x - 1)^2} + {(y - 2)^2} + \) \({(z - 3)^2} = 9\) tâm \(I\) và mặt phẳng \((P):2x + 2y - z + 24 = 0\). Gọi \(H\) là hình chiếu vuông góc của \(I\) trên \((P)\). Điểm \(M\) thuộc \((S)\) sao cho đoạn $M H$ có độ dài lớn nhất. Tìm tọa độ điểm \(M\).
Trả lời bởi giáo viên
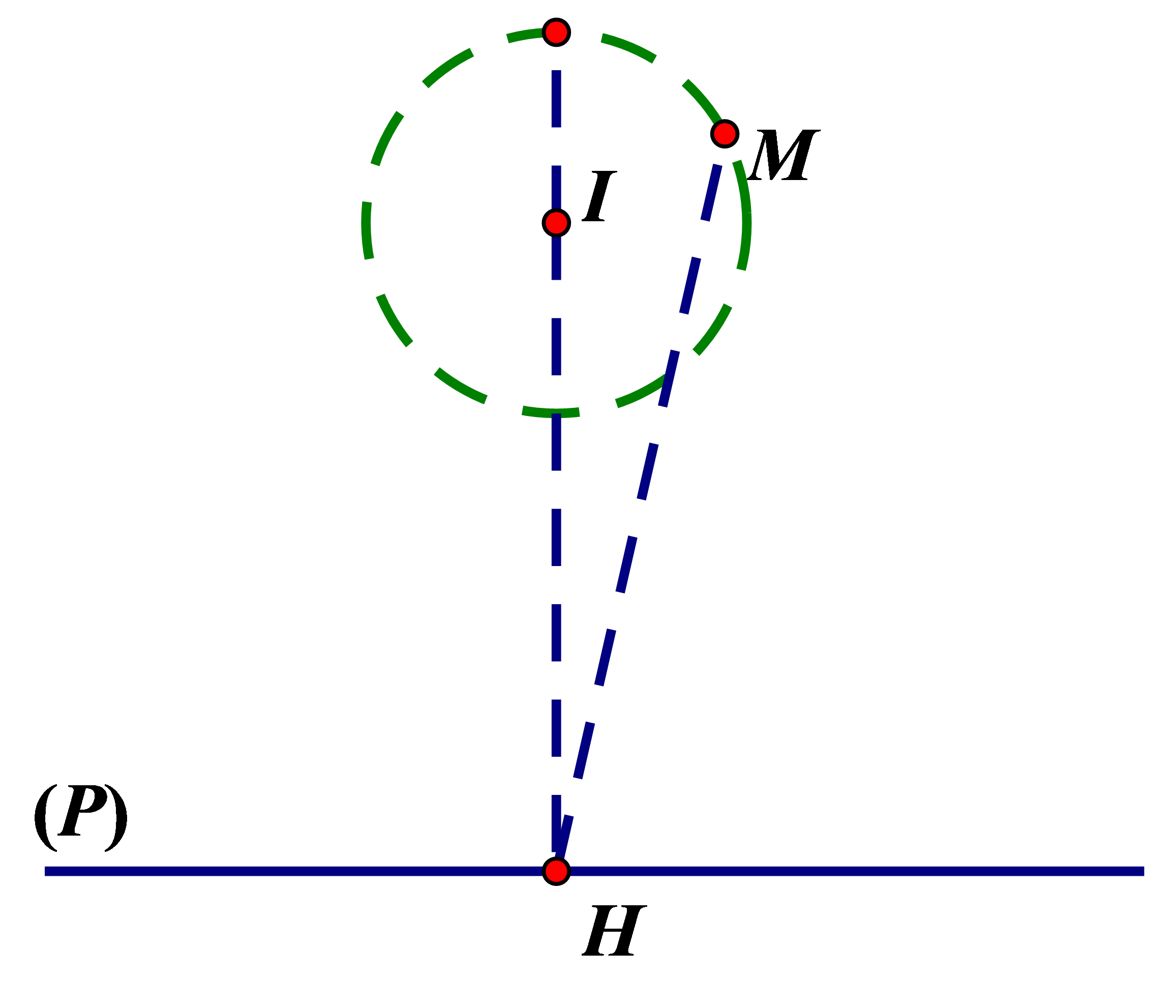
Bước 1: Tìm phương trình IH
Ta có tâm \(I(1;2;3)\) và bán kính \(R = 3\). Do \(d(I;(P)) = 9 > R\) nên mặt phẳng \(M\) lớn nhất nên \(M\) \((P)\) không cắt mặt cầu \((S)\). Do \(H\) là hình chiếu của \(I\) lên (P) và MH lớn nhất nên M là giao điểm của đường thẳng IH với mặt cầu (S). Đường thẳng IH nhận \(\overrightarrow {{n_{(P)}}} = (2;2; - 1)\) làm vecto chỉ phương. Phương trình đường thẳng IH là:
\(\left\{ {\begin{array}{*{20}{l}}{x = 1 + 2t}\\{y = 2 + 2t.}\\{z = 3 - t}\end{array}} \right.\)
Bước 2: Tìm M.
Vì M là giao điểm của đường thẳng IH với mặt cầu (S)\( \Rightarrow 9{t^2} = 9 \Leftrightarrow t = \pm 1\)\( \Rightarrow {M_1}\left( {3;4;2} \right)\) và \({M_2}( - 1;0;4).\)
\({M_1}H = d\left( {{M_1};(P)} \right) = 12;{M_2}H = d\left( {{M_2};(P)} \right) = 6\). Vậy điểm cần tìm là \(M(3;4;2)\).
Hướng dẫn giải:
Bước 1: Tìm phương trình IH
Bước 2: Tìm M.

