Trong không gian Oxyz, cho \((P):x + 2y - 2z + 5 = 0\) và 2 mặt cầu \(\left( {{S_1}} \right)\):\({(x - 2)^2} + {y^2} + {(z + 1)^2} = 1,\)\(\left( {{S_2}} \right):{(x + 4)^2} + {(y + 2)^2} + {(z - 3)^2} = 4\). Gọi M, A, B lần lượt thuộc mặt phẳng \((P)\) và hai mặt cầu \(\left( {{S_1}} \right),\left( {{S_2}} \right)\). Tìm giá trị nhỏ nhất của \(S = MA + MB.\)
Trả lời bởi giáo viên
Bước 1: Xác định các yếu tố của \(\left( P \right),\left( {{S_1}} \right),\left( {{S_2}} \right)\)
Mặt phẳng \((P)\) có một vectơ pháp tuyến là \(\overrightarrow {{n_P}} = (1;2; - 2)\).
Mặt cầu \(\left( {{S_1}} \right)\) có tâm \({I_1}(2;0; - 1)\) và bán kính \({R_1} = 1\).
Mặt cầu \(\left( {{S_2}} \right)\) có tâm \({I_2}( - 4; - 2;3)\) và bán kính \({R_2} = 2\).
Bước 2: Nhận xét vị trí tương đối của \(\left( {{S_1}} \right),\left( {{S_2}} \right)\) so với nhau và vị trí của hai điểm \({I_1},{I_2}\) đối với mặt phẳng \((P)\)
Ta có \(\overrightarrow {{I_1}{I_2}} = ( - 6; - 2;4)\)\( \Rightarrow {I_1}{I_2} = 2\sqrt {14} > {R_1} + {R_2}\) suy ra \(\left( {{S_1}} \right),\left( {{S_2}} \right)\) nằm ngoài nhau.
Ta có \(\left( {{x_{{I_1}}} + 2{y_{{I_1}}} - 2{z_{{I_1}}} + 5} \right)\)\(\left( {{x_{{I_2}}} + 2{y_{{I_2}}} - 2{z_{{I_2}}} + 5} \right) < 0\) nên \({I_1},{I_2}\) nằm về hai phía đối với mặt phẳng \((P)\).
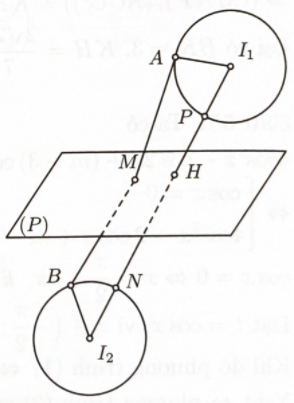
Bước 3: Gọi P, N, H lần lượt là giao điểm của đoạn thẳng \({I_1}{I_2}\) với hai mặt cầu \(\left( {{S_1}} \right),\left( {{S_2}} \right)\) và \((P)\). Tìm \({(MA + MB)_{\min }}\)
Ngoài га \(d\left[ {{I_1},(P)} \right] = 3 > {R_1},d\left[ {{I_2},(P)} \right] = 3 > {R_2}\).
Gọi P, N, H lần lượt là giao điểm của đoạn thẳng \({I_1}{I_2}\) với hai mặt cầu \(\left( {{S_1}} \right),\left( {{S_2}} \right)\) và \((P)\).
$AI_1=PI_1;BI_2=NI_2$
$I_1I_2=I_1P+PN+NI_2$
Ta có \(MA + MB + A{I_1} + B{I_2} \ge {I_1}{I_2}\)
\( \Leftrightarrow MA + MB + P{I_1} + N{I_2}\)\( \ge {I_1}P + PN + N{I_2}\)\( \Leftrightarrow MA + MB \ge NP\)
Đẳng thức xảy ra khi và chỉ khi \(A \equiv P,B \equiv N\) và \(M \equiv H.\)
Khi đó, \({(MA + MB)_{\min }} = NP = {I_1}{I_2} - {R_1} - {R_2}\)\( = 2\sqrt {14} - 3\)
Hướng dẫn giải:
Bước 1: Xác định các yếu tố của \(\left( P \right),\left( {{S_1}} \right),\left( {{S_2}} \right)\)
Bước 2: Nhận xét vị trí tương đối của \(\left( {{S_1}} \right),\left( {{S_2}} \right)\) so với nhau và vị trí của hai điểm \({I_1},{I_2}\) đối với mặt phẳng \((P)\)
Bước 3: Gọi P, N, H lần lượt là giao điểm của đoạn thẳng \({I_1}{I_2}\) với hai mặt cầu \(\left( {{S_1}} \right),\left( {{S_2}} \right)\) và \((P)\). Tìm \({(MA + MB)_{\min }}\)

