Tìm m để hàm số $y = \sqrt {8\cos x - 6\sin x - {{\left( {3\sin x - 4\cos x} \right)}^2} - 2m}$ có tập xác định là R.

Bước 1:

Ta có $y = \sqrt {8\cos x - 6\sin x - {{\left( {3\sin x - 4\cos x} \right)}^2} - 2m}$

Hàm số trên có tập xác định R khi

$\begin{array}{l}8\cos x - 6\sin x - {\left( {3\sin x - 4\cos x} \right)^2} - 2m \ge 0\\ \Leftrightarrow 2\left( {4\cos x - 3\sin x} \right) - {\left( {3\sin x - 4\cos x} \right)^2} - 2m \ge 0\end{array}$

Bước 2:

Đặt $t = 4\cos x - 3\sin x$

Theo BĐT Bu-nhi-a-cốp-xki ta có:

${t^2} = {\left( {4\cos x - 3\sin x} \right)^2}$$\le \left( {{4^2} + {3^2}} \right)\left( {{{\sin }^2}x + {{\cos }^2}x} \right) = 25$$\Leftrightarrow  - 5 \le t \le 5$

Bước 3:

Ta có bất phương trình $2t - {t^2} - 2m \ge 0\forall t \in \left[ { - 5;5} \right]$

$\Leftrightarrow  - 2m \ge {t^2} - 2t\forall t \in \left[ { - 5;5} \right]$(1)

Bước 4:

Xét hàm số $f\left( t \right) = {t^2} - 2t$ trên $\left[ { - 5;5} \right]$

Ta có $-\dfrac{b}{2a}=1 \in \left[ { - 5;5} \right]$

Vì $a=1>0$ nên hàm số nghịch biến trên $(-\infty;1)$ và đồng biến trên $(1;+\infty)$

Mà $(-5;1) \subset (-\infty;1)$ và $(1;5) \subset (1;+\infty)$ nên hàm số nghịch biến trên $(-5;1)$ và đồng biến trên $(1;5)$.

Bảng biến thiên:

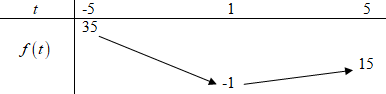
Bước 5:

Dựa vào bảng biến thiên ta thấy bất đẳng thức (1) xảy ra khi $- 2m \ge 35 \Leftrightarrow m \le  - \dfrac{{35}}{2}$