Câu hỏi:
2 năm trước
Một phân xưởng đặt kế hoạch sản xuất $200$ sản phẩm. Trong \(5\) ngày đầu do còn làm việc khác nên mỗi ngày phân xưởng sản xuất ít hơn mức đề ra là \(4\) sản phẩm. Trong những ngày còn lại, xưởng sản xuất vượt mức \(10\) sản phẩm mỗi ngày nên hoàn thành kế hoạch sớm hơn \(1\) ngày. Hỏi theo kế hoạch, mỗi ngày phân xưởng cần sản xuất bao nhiêu sản phẩm.
Trả lời bởi giáo viên
Đáp án đúng: d
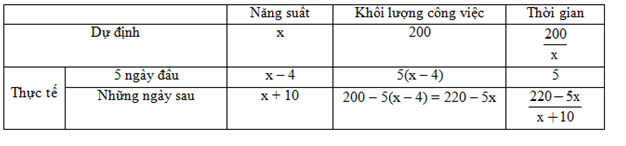
Gọi năng suất làm việc theo dự kiến của xí nghiệp là $x$ (sản phẩm/ngày) , $\left( {x{\rm{ }} > {\rm{ }}4} \right)$
+) Theo dự kiến: Mỗi ngày phân xưởng sản xuất x sản phẩm, tổng sản phẩm là 200 sản phẩm và thời gian sản xuất là $\dfrac{{200}}{x}$ ngày
+ Thực tế: $5$ ngày đầu phân xưởng sản xuất $x--4$ (sản phẩm/ngày), số sản phẩm sản xuất được là $5\left( {x--4} \right).$ Những ngày sau mỗi ngày phân xưởng sản xuất $x + 10$ (sản phẩm/ngày), số sản phẩm sản xuất được là $220--5x$ với thời gian sản xuất là $\dfrac{{220 - 5{\rm{x}}}}{{x + 10}}$ (ngày)
*) Vì thực tế xí nghiệp đã hoàn thành công việc sớm 1 ngày sovới dự định nên ta có phương trình: $\dfrac{{200}}{x} = 5 + \dfrac{{220 - 5{\rm{x}}}}{{x + 10}} + 1$ $ \Leftrightarrow \dfrac{{200}}{x} = 6 + \dfrac{{220 - 5{\rm{x}}}}{{x + 10}}$
$ \Leftrightarrow 200(x + 10) = 6{\rm{x}}(x + 10) + x(220 - 5x)$$ \Leftrightarrow {x^2} + 80{\rm{x}} - 2000 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 20(t/m)\\x = - 100(l)\end{array} \right.$
Vậy theo dự kiến mỗi ngày phân xưởng sản xuất $20$ sản phẩm
Hướng dẫn giải:
Lập bảng như sau:
Phương trình: $\dfrac{{200}}{x} = 5 + \dfrac{{220 - 5{\rm{x}}}}{{x + 10}} + 1$
Câu hỏi khác
- Bài tập hàm số bậc hai một ẩn và đồ thị hàm số y=ax^2 toán 9 có lời giải
- Bài tập hệ thức vi-ét và ứng dụng toán 9 có lời giải
- Bài tập phương trình bậc hai một ẩn và công thức nghiệm toán 9 có lời giải
- Bài tập công thức nghiệm thu gọn toán 9 có lời giải
- Bài tập phương trình quy về phương trình bậc hai toán 9 có lời giải
