Câu hỏi:
2 năm trước
Ký hiệu \(M\) và \(m\) tương ứng là GTLN và GTNN của hàm số \(y = {x^2} - 2x + 5\) trên miền \(\left[ {2;7} \right].\) Biết rằng M=km. Tìm k?
Đáp án:
Trả lời bởi giáo viên
Đáp án:
Đáp án:
Bước 1:
Xét hàm số \(y = {x^2} - 2x + 5\) trên \(\left[ {2;\,\,7} \right]\) ta có BBT:
Đỉnh của đồ thị hàm số \(y = {x^2} - 2x + 5\) là \(I\left( {1;\,\,4} \right)\)
Ta thấy $1 \notin [2;7]$. Ta lập bảng biến thiên:
Bước 2:
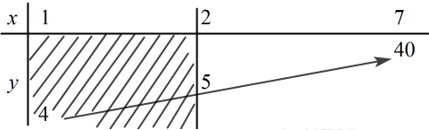
Dựa vào BBT ta có: \(M = \mathop {Max}\limits_{\left[ {2;\,\,7} \right]} y = 40\) khi \(x = 7\) và \(m = \mathop {Min}\limits_{\left[ {2;\,\,7} \right]} y = 5\) khi \(x = 2.\)
\( \Rightarrow M = 8m\)
Hướng dẫn giải:
Bước 1: Xác định hoành độ đỉnh \({x_I}\) xem có thuộc đoạn \(\left[ {a;b} \right]\) cần tìm GTLN, GTNN hay không?
Bước 2: Nếu \({x_I} \notin \left[ {a;b} \right]\) thì ta tính \(f\left( a \right);f\left( b \right)\) và so sánh ta được GTLN, GTNN.
