Trả lời bởi giáo viên
Đáp án đúng: b
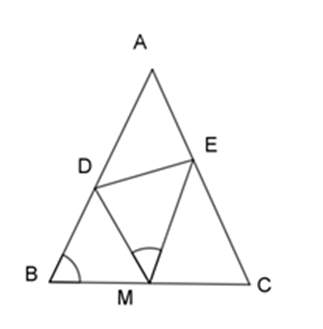
Ta có: ΔBDM∽ (chứng minh trên)
\Rightarrow \dfrac{{DM}}{{ME}} = \dfrac{{BD}}{{CM}} = \dfrac{{BD}}{{BM}} (do CM = BM (gt))
\Rightarrow \dfrac{{BD}}{{DM}} = \dfrac{{BM}}{{ME}}
Xét \Delta BDM và \Delta MDE ta có:
\dfrac{{BD}}{{DM}} = \dfrac{{BM}}{{ME}}
\widehat {DME} = \widehat {ABC} (gt)
\Rightarrow \Delta BDM\backsim\Delta MDE\;(c - g - c)
\Rightarrow \widehat {BDM} = \widehat {MDE} (hai góc tương ứng)
Hướng dẫn giải:
Từ hai tam giác đồng dạng đã biết suy ra tỉ lệ cạnh thích hợp để chứng minh \Delta BDM\backsim\Delta MDE\;(c - g - c)
để suy ra hai góc bằng nhau.
Câu hỏi khác
- Bài tập định lý Ta-lét. Định lý đảo và hệ quả của định lý Ta-lét toán 8 có lời giải
- Bài tập tính chất đường phân giác của tam giác toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ nhất toán 8 có lời giải
- Bài tập hai tam giác đồng dạng toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ hai toán 8 có lời giải
