Trả lời bởi giáo viên
Đáp án đúng: a
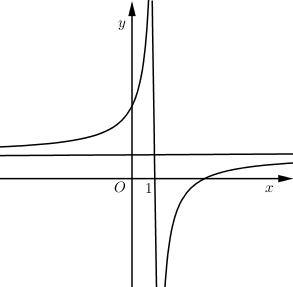
+) y=ax−bx−1⇒y′=−a+b(x−1)2,∀x≠1
Hàm số đồng biến ⇒y′>0⇔−a+b>0⇔b>a
+) Tiệm cận ngang y=a1>0⇒a>0
Vậy 0<a<b
Hướng dẫn giải:
- Xét tính đơn điệu của hàm số suy ra điều kiện của a,b.
- Tìm tiệm cận ngang của đồ thị hàm số suy ra điều kiện của a.