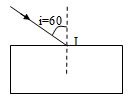
Đặt một khối chất trong suốt có 2 mặt song song, bề dầy \(e =2cm\) trong không khí. Từ không khí chiếu một chùm sáng hỗn hợp gồm 2 ánh sáng đơn sắc \({\lambda _1}\) và \({\lambda _2}\) coi như một tia sáng tới mặt trên khối chất dưới góc tới \(i = {60^0}\) như hình vẽ bên. Biết chiết suất của khối chất đó đối với ánh sáng \({\lambda _1}\) và \({\lambda _2}\) lần lượt là \({n_1} = \sqrt 3 \) và \({n_2} = \sqrt 2 \). Khoảng cách giữa 2 tia ló ra ở mặt dưới của khối chất là:
Trả lời bởi giáo viên
Theo định luật khúc xạ ánh sáng ta vẽ được đường đi qua khối chất trong suốt trên của tia sáng như hình vẽ.
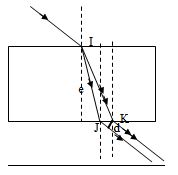
Dễ thấy sau khi bị tán sắc ở mặt trên và ló ra ở mặt dưới của khối chất thì 2 tia đơn sắc \({\lambda _1}\) và \({\lambda _2}\) song song với nhau.
Từ hình vẽ ta có khoảng cách giữa 2 tia ló là:
\(d = JK.sin\left( {90 - i} \right) = e.\left( {tan{r_2} - tan{r_1}} \right).sin\left( {90 - i} \right)\left( 1 \right)\)
Với \(i = {60^0}\); \({r_2} = \arcsin \left( {\dfrac{{{\rm{sini}}}}{{{{\rm{n}}_{\rm{2}}}}}} \right) = {\rm{ }}arcsin\left( {\dfrac{{{\rm{sin 60}}}}{{\sqrt 2 }}} \right)\); \({r_1} = arcsin\left( {\dfrac{{{\rm{sin 60}}}}{{\sqrt 3 }}} \right)\); \(e{\rm{ }} = {\rm{ }}2cm\) ;
Thay vào (1) ta được: \(d = {\rm{ }}0,1972cm\)
Hướng dẫn giải:
Định luật khúc xạ ánh sáng \({n_1}sini{\rm{ }} = {\rm{ }}{n_2}sinr\)