Thí nghiệm giao thoa ánh sáng đơn sắc với hai khe \({S_1},{S_2}\) như hình vẽ.
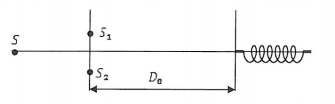
Màn quan sát gắn với lò xo và có thể dao động điều hòa với chu kì riêng \(T{\rm{ }} = {\rm{ }}1,5s\). Bỏ qua ma sát và sức cản môi trường. ban đầu màn nằm cân bằng và khoảng cách từ hai khe đến màn là \({D_0}\) ta thu được một hệ vân giao thoa mà điểm M trên màn cách vân sáng trung tâm \(3\left( {mm} \right)\) là vân sáng bậc \(3\). Đưa màn đến vị trí lò xo nén \(\Delta l = \dfrac{{{D_0}}}{{\sqrt 2 }}\) rồi thả nhẹ cho dao động. Sau bao lâu thì tại M ta thu được vân sáng bậc \(2\) lần đầu:
Trả lời bởi giáo viên
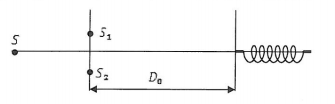
Ban đầu khoảng cách từ 2 khe đến màn quan sát là \({D_0}\) thì tại M cách vân trung tâm 3mm là vân sáng bậc 3 nên ta có \({x_M} = k\frac{{\lambda {D_0}}}{a} = 3.\frac{{\lambda {D_0}}}{a}\) (1)
Vì đây là con lắc lò xo nằm ngang nên khi đưa màn quan sát đến vị trí lò xo bị nén \(\Delta l = \frac{{{D_0}}}{{\sqrt 2 }}\) rồi buông nhẹ thì ta cũng có \(A = \frac{{{D_0}}}{{\sqrt 2 }}\)
Khi M là vân sáng bậc 2 thì gọi D là khoảng cách từ 2 khe đến màn quan sát ta có: \({x_M} = k\frac{{\lambda D}}{a} = 2.\frac{{\lambda D}}{a}\) (2)
Từ (1) và (2) ta có: \(3\frac{{\lambda {D_0}}}{a} = 2\frac{{\lambda D}}{a} \Leftrightarrow D = \frac{3}{2}{D_0}\)
Khoảng thời gian từ thời điểm thả nhẹ màn cho dao động đến khi M trở thành vân sáng bậc 2 lần đầu chính là khoảng thời gian ngắn nhất để màn dao động từ biên độ A đến điểm B tức là khi đó màn dao động từ biên đến vị trí cách vị trí cân bằng 1 khoảng \(\frac{{\sqrt 2 }}{2}A\) nên ta có \(t = \frac{T}{8} = \frac{{1,5}}{8} = \frac{3}{{16}}s\)
Hướng dẫn giải:
Sử dụng công thức xác định vị trí vân sáng: \({x_S} = ki = k\dfrac{{\lambda D}}{a}\)

