Thực hiện giao thoa khe Y-âng với hai bức xạ đơn sắc \({\lambda _1}\) và \({\lambda _2}\) thì khoảng vân tương ứng là \({i_1} = {\rm{ }}0,3{\rm{ }}mm\) và \({i_2} = {\rm{ }}0,4{\rm{ }}mm\) . Gọi \(A\) và \(B\) là hai điểm trên màn quan sát, nằm cùng một phía so với vân trung tâm và cách nhau \(3mm\). Biết tại \(A\) là vị trí vân sáng trùng nhau của hai bức xạ, nếu vị trí vân sáng trùng nhau chỉ tính một vân sáng thì số vân sáng quan sát được trên đoạn \(AB\) (kể cả \(A\) và \(B\)) là:
Trả lời bởi giáo viên
+ Số vân sáng của bức xạ đơn sắc 1 thu được trên màn \({N_1} = 2\left[ {\dfrac{L}{{2{i_1}}}} \right] + 1 = 11\)
+ Số vân sáng của bức xạ đơn sắc 2 thu được trên màn \({N_2} = 8\) (Tính cả vị trí tại A vì tại đó bức xạ 1 và 2 cùng cho vân sáng)
+ Xét sự trùng nhau của hai bức xạ \(\dfrac{{{k_1}}}{{{k_2}}} = \dfrac{{{i_2}}}{{{i_1}}} = \dfrac{4}{3} \Rightarrow {x_{tr}} = 4{i_1} = 3{i_2} = 1,2mm\)
+ Số vân sáng trùng nhau của hai bức xạ là \({N_{tr}} = 2\left[ {\dfrac{L}{{2{x_{tr}}}}} \right] + 1 = 3\)
Vẽ trên hình ta được:
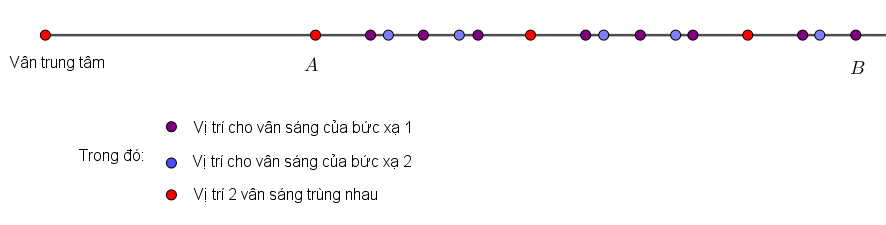
=> Số vân sáng quan sát được trên màn là: \(N=N_1+N_2-N_{tr}=11+8-3=16\) vân sáng
Hướng dẫn giải:
Sử dụng lí thuyết bài toán giao thoa nhiều ánh sáng