Câu hỏi:
2 năm trước
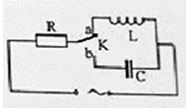
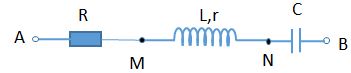
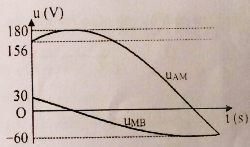
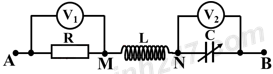
Đặt điện áp xoay chiều ổn định vào hai đầu đoạn mạch AB như hình vẽ. Biết cuộn dây L thuần cảm, tụ điện có điện dung C thay đổi được. Các vôn kế V1, V2 lý tưởng. Điều chỉnh giá trị của C thì thấy ở cùng thời điểm số chỉ của V1 cực đại thì số chỉ của V1 gấp đôi số chỉ của V2. Hỏi khi số chỉ của V2 cực đại và có giá trị V2max = 200 V thì số chỉ của V1 là
Trả lời bởi giáo viên
Đáp án đúng: a
+ Khi \(C = {C_0}\) thì: \({V_{1max}}\) khi đó mạch xảy ra cộng hưởng
\({V_{1max}} = {U_R} = {U_{AB}}\) và \({Z_L} = {Z_{{C_0}}}\)
Tại đây, ta có: \({U_R} = 2{U_{{C_0}}} \Rightarrow {U_{{C_0}}} = \dfrac{{{U_{AB}}}}{2} = {U_L}\)
\( \Rightarrow {Z_L} = {Z_{{C_0}}} = \dfrac{R}{2}\)
+ Khi \(C = C'\) thì \({V_{2max}}\) khi đó \({V_{2max}} = {U_{{C_{max}}}} = \dfrac{{{U^2}\sqrt {{R^2} + Z_L^2} }}{R}\) (1)
Và \({Z_{C'}} = \dfrac{{{R^2} + Z_L^2}}{{{Z_L}}} = \dfrac{{{R^2} + \dfrac{{{R^2}}}{4}}}{{\dfrac{R}{2}}} = \dfrac{5}{2}R\)
Thay vào (1) ta có: \(200 = \dfrac{{U\sqrt {{R^2} + \dfrac{{{R^2}}}{4}} }}{R} \Rightarrow U = 80\sqrt 5 V\)
Số chỉ vôn kế \({V_1}\) khi đó là \({V_1} = {U_R} = I.R = \dfrac{U}{Z}.R\)
\({V_1} = \dfrac{{80\sqrt 5 }}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_{C'}}} \right)}^2}} }}R = \dfrac{{80\sqrt 5 }}{{\sqrt {{R^2} + {{\left( {\dfrac{R}{2} - \dfrac{5}{2}R} \right)}^2}} }}R = 80V\)
Hướng dẫn giải:
+ Bài toán C biến thiên để \({U_{{R_{max}}}}\)
+ Bài toán C biến thiên để \({U_{{C_{max}}}}\)
Câu hỏi khác
- Bài tập mạch RLC mắc nối tiếp có lời giải MÔN LÝ lớp 12
- Bài tập các mạch điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập pha u,i - viết phương trình u, i có lời giải MÔN LÝ lớp 12
- Bài tập lý thuyết đại cương về dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập đại cương dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
