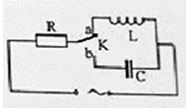
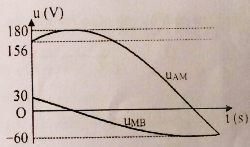
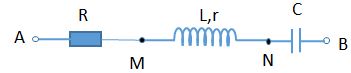
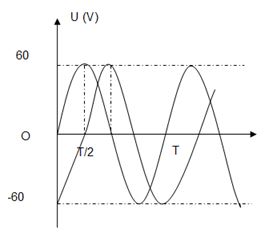
Đặt điện áp xoay chiều \(u = {U_0}{\rm{cos}}\left( {\dfrac{{2\pi }}{T}t + \varphi } \right)V\) vào hai đầu đoạn mạch \(AB\) như hình bên. Biết \(R{\rm{ }} = {\rm{ }}r\). Đồ thị biểu diễn điện áp \({u_{AN}}\) và \({u_{MB}}\) như hình vẽ bên cạnh. Giá trị của U0 bằng:
Trả lời bởi giáo viên
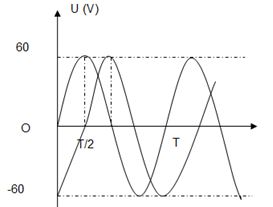
Từ đồ thị ta thấy được các giá trị
Tại thời điểm ban đầu \(t{\rm{ }} = {\rm{ }}0\), thì điện áp trên đoạn \(AN\) bằng \(0\), điện áp trên đoạn \(MB\) đạt cực tiểu (ở biên âm), dao động với cùng chu kì, nên ta thấy được điện áp trên đoạn mạch \(MB\) trễ pha so với điện áp trên đoạn mạch \(AN\) một góc là \(\dfrac{\pi }{2}\). Hay điện áp tức thời trên hai đoạn mạch này vuông pha với nhau. Mặt khác \(R{\rm{ }} = {\rm{ }}r\) nên ta có
Ta vẽ được giản đồ vecto như sau:
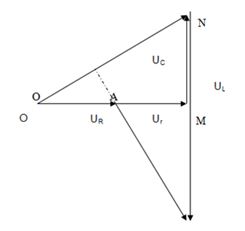
Tam giác \(OMN\) bằng với tam giác \(BMA\) theo trường hợp cạnh huyền và góc vuông (\(ON{\rm{ }} = {\rm{ }}AB\); \(\widehat O = \widehat B\))
Từ đó suy ra được :
\( \to {U_{R0}} = {U_{r0}} = \dfrac{{60}}{{\sqrt 5 }}V\)
\(U_0^2 = {\left( {2{U_{r0}}} \right)^2} + {(2{U_{r0}})^2} = \dfrac{{{{8.60}^2}}}{5} \Rightarrow {U_0} = \dfrac{{120\sqrt 2 }}{{\sqrt 5 }} = 75,89V\)
Hướng dẫn giải:
Vẽ giản đồ vec tơ của mạch điện, sử dụng các tính chất hình học