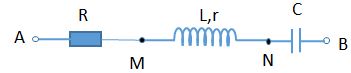
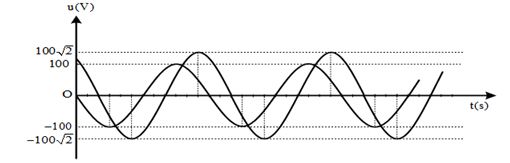
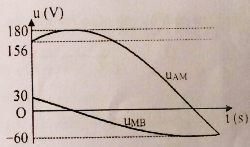
Đặt điện áp xoay chiều vào hai đầu đoạn mạch \(AB\) gồm: đoạn mạch \(AM\)chứa điện trở thuần \(R = 90\Omega \) và tụ điện \(C = 35,4\mu F\), đoạn mạch \(MB\) gồm hộp \(X\) chứa \(2\) trong \(3\) phần tử mắc nối tiếp (điện trở thuần \({R_0}\); cuộn cảm thuần có độ tự cảm \({L_0}\); tụ điện có điện dung \({C_0}\)). Khi đặt vào hai đầu \(AB\) một điện thế xoay chiều có tần số \(50Hz\) thì ta được đồ thị sự phụ thuộc của \({u_{AM}}\) và \({u_{MB}}\) theo thời gian như hình vẽ (chú ý \(90\sqrt 3 {\rm{}} \approx 156\) ). Giá trị của các phần tử trong hộp \(X\) là:

Một mạch điện xoay chiều có dạng như hình vẽ trong đó cuộn dây thuần cảm có cảm kháng \({Z_L} = 0,5R\), tụ điện có dung kháng \({Z_C} = 2R\). Khi khóa K đặt ở a, thì cường độ dòng điện qua cuộn dây có biểu thức \({i_1} = 0,4\sin \left( {100\pi t + \dfrac{\pi }{6}} \right)A\). Hỏi khi khóa K đặt tại b thì dòng điện qua C có biểu thức nào sau đây ?

Đặt điện áp xoay chiều \(u = U\sqrt 2 {\rm{cos2}}\pi {\rm{ft}}\left( V \right)\) vào hai đầu đoạn mạch gồm điện trở \(R\), cuộn cảm thuần \(L\) và tụ điện \(C\) mắc nối tiếp nhau. Hệ số công suất của đoạn mạch khi đó là \(k\). Khi nối hai đầu cuộn cảm bằng một dây dẫn có điện trở không đáng kể thì điện áp hiệu dụng trên điện trở \(R\) tăng \(2\sqrt 2 \) lần và cường độ dòng điện qua đoạn mạch trong hai trường hợp lệch pha nhau một góc \(\dfrac{\pi }{2}\) . Giá trị của k bằng:

Đặt điện áp xoay chiều vào mạch điện \(AB\) gồm ba đoạn mạch nối tiếp: \(AM\) có cuộn dây thuần cảm với hệ số tự cảm \({L_1}\) ; \(MN\) có cuộn dây có hệ số tự cảm \({L_2}\); \(NB\) có tụ điện với điện dung \(C\). Biết điện áp tức thời trên \(MN\) trễ pha \(\dfrac{\pi }{6}\) so với điện áp trên \(AB\), \({U_{MN}} = {\text{ }}2{U_C}\) , \({Z_{L1}} = {\text{ }}5{Z_C}\). Hệ số công suất của đoạn mạch \(MN\) gần với giá trị nào sau đây nhất?

Đặt điện áp xoay chiều \(u = {U_0}{\rm{cos}}\left( {\dfrac{{2\pi }}{T}t + \varphi } \right)V\) vào hai đầu đoạn mạch \(AB\) như hình bên. Biết \(R{\rm{ }} = {\rm{ }}r\). Đồ thị biểu diễn điện áp \({u_{AN}}\) và \({u_{MB}}\) như hình vẽ bên cạnh. Giá trị của U₀ bằng:

Mạch điện \(AB\) gồm đoạn \(AM\) và đoạn \(MB\): Đoạn \(AM\) có một điện trở thuần \(50\Omega \) và đoạn \(MB\) có một cuộn dây. Đặt vào mạch \(AB\) một điện áp xoay chiều thì điện áp tức thời của hai đoạn \(AM\) và \(MB\) biến thiên như trên đồ thị:  

Cảm kháng của cuộn dây là:

Trên đoạn mạch không phân nhánh có bốn điểm theo đúng thứ tự \(A,{\rm{ }}M,{\rm{ }}N,{\rm{ }}B\). Giữa \(A\) và \(M\) chỉ có điện trở thuần. Giữa \(M\) và \(N\) chỉ có cuộn dây. Giữa \(N\) và \(B\) chỉ có tụ điện. Đặt vào hai đầu đoạn mạch \(AB\) một điện áp xoay chiều có hiệu điện thế hiệu dụng \(U\). Khi đó công suất tiêu thụ trên đoạn mạch \(AM\) bằng công suất tiêu thụ trên đoạn mạch \(MN\). Sự phụ thuộc của hiệu điện thế tức thời hai đầu \(AN\) và \(MB\) theo thời gian được cho như trên đồ thị. Giá trị của \(U\) xấp xỉ bằng: