Câu hỏi:
2 năm trước
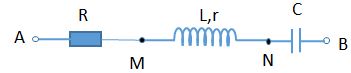
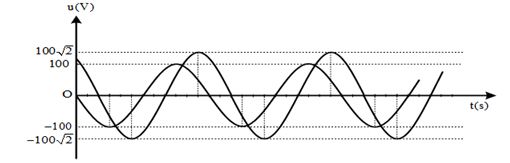
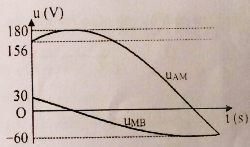
Trên đoạn mạch không phân nhánh có bốn điểm theo đúng thứ tự \(A,{\rm{ }}M,{\rm{ }}N,{\rm{ }}B\). Giữa \(A\) và \(M\) chỉ có điện trở thuần. Giữa \(M\) và \(N\) chỉ có cuộn dây. Giữa \(N\) và \(B\) chỉ có tụ điện. Đặt vào hai đầu đoạn mạch \(AB\) một điện áp xoay chiều có hiệu điện thế hiệu dụng \(U\). Khi đó công suất tiêu thụ trên đoạn mạch \(AM\) bằng công suất tiêu thụ trên đoạn mạch \(MN\). Sự phụ thuộc của hiệu điện thế tức thời hai đầu \(AN\) và \(MB\) theo thời gian được cho như trên đồ thị. Giá trị của \(U\) xấp xỉ bằng:
Trả lời bởi giáo viên
Đáp án đúng: d
Dựa vào đồ thị và dữ kiện đề bài: \(\left\{ \begin{array}{l}R = r \Rightarrow {U_R} = {U_r}\\\overrightarrow {{U_{AN}}} \bot \overrightarrow {{U_{MB}}} \end{array} \right.\)
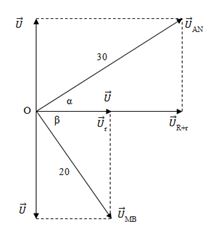
Ta có: \(\alpha {\rm{}} + \beta {\rm{}} = \dfrac{{\pi {\rm{}}}}{2} \Rightarrow c{\rm{os}}\beta {\rm{}} = \sin \alpha {\rm{}} \Rightarrow \dfrac{{{U_R}}}{{20}} = \dfrac{{{U_L}}}{{30}} \Rightarrow {U_L} = \dfrac{{{U_R}.30}}{{20}} = 1,5{U_R} \Rightarrow {Z_L} = 1,5R\)
\(\begin{array}{l}\dfrac{{U_{MB}^2}}{{U_{AN}^2}} = \dfrac{{Z_{MB}^2}}{{Z_{AN}^2}} = \dfrac{{{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}{{{{\left( {2R} \right)}^2} + Z_L^2}} = \dfrac{{{{20}^2}}}{{{{30}^2}}} = \dfrac{4}{9} \Leftrightarrow \dfrac{{{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}{{{{\left( {2R} \right)}^2} + {{\left( {1,5R} \right)}^2}}} = \dfrac{4}{9} \Rightarrow {\left( {{Z_L} - {Z_C}} \right)^2} = \dfrac{{16}}{9}{R^2}\\\dfrac{{{U^2}}}{{U_{AN}^2}} = \dfrac{{Z_{MB}^2}}{{Z_{AN}^2}} = \dfrac{{{{\left( {2R} \right)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}{{{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}} \Leftrightarrow \dfrac{{{U^2}}}{{{{20}^2}}} = \dfrac{{4{R^2} + \dfrac{{16}}{9}{R^2}}}{{{R^2} + \dfrac{{16}}{9}{R^2}}} \Rightarrow U = 28,8V\end{array}\)
Hướng dẫn giải:
Sử dụng giản đồ véc–tơ
Câu hỏi khác
- Bài tập các mạch điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập mạch RLC mắc nối tiếp có lời giải MÔN LÝ lớp 12
- Bài tập pha u,i - viết phương trình u, i có lời giải MÔN LÝ lớp 12
- Bài tập lý thuyết đại cương về dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập đại cương dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
