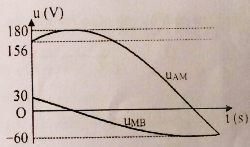
Đặt điện áp xoay chiều \(u = U\sqrt 2 {\rm{cos2}}\pi {\rm{ft}}\left( V \right)\) vào hai đầu đoạn mạch gồm điện trở \(R\), cuộn cảm thuần \(L\) và tụ điện \(C\) mắc nối tiếp nhau. Hệ số công suất của đoạn mạch khi đó là \(k\). Khi nối hai đầu cuộn cảm bằng một dây dẫn có điện trở không đáng kể thì điện áp hiệu dụng trên điện trở \(R\) tăng \(2\sqrt 2 \) lần và cường độ dòng điện qua đoạn mạch trong hai trường hợp lệch pha nhau một góc \(\dfrac{\pi }{2}\) . Giá trị của k bằng:
Trả lời bởi giáo viên
Ban đầu mạch gồm RLC mắc nối tiếp, ta gọi các giá trị điện áp trên các phần tử là \({U_R};{\rm{ }}{U_L};{\rm{ }}{U_{\bf{C}}}\)
Lúc sau, mạch được nối tắt qua L, nên chỉ còn R và C nối tiếp, ta gọi các điện áp trên các phần tử là \(U{'_L}\) và \(U{'_{\bf{C}}}\)
Biết rằng lúc sau dòng điện tức thời lệch pha \(\frac{\pi }{2}\) so với cường độ dòng điện lúc đầu, ta có: \(\left\{ \begin{array}{l}{\varphi _{i1}} = {\varphi _u} - {\varphi _1}\\{\varphi _{i2}} = {\varphi _u} - {\varphi _2}\end{array} \right. \Rightarrow {\varphi _{i1}} - {\varphi _{i2}} = \dfrac{\pi }{2} \Rightarrow {\varphi _2} - {\varphi _1} = \dfrac{\pi }{2}\)
Ta vẽ trên cùng 1 giản đồ véc-tơ:
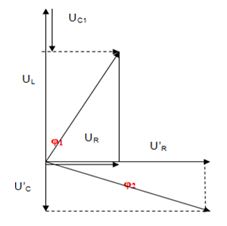
Ta có: \({\varphi _1} + \left| {{\varphi _2}} \right| = \dfrac{{\pi {\rm{}}}}{2};\cos {\varphi _1} = \dfrac{{{U_R}}}{{{U_{AB}}}} = k;\cos {\varphi _2} = {\rm{ }}\dfrac{{{U_R}}}{{{U_{AB}}}} = \dfrac{{2.\sqrt 2 .{U_R}}}{{{U_{AB}}}} = 2\sqrt 2 .k\)
Mặt khác :
\({\varphi _1} + \left| {{\varphi _2}} \right| = \dfrac{{\pi {\rm{}}}}{2} \Rightarrow \cos {\varphi _1} = \sin {\varphi _2} \Leftrightarrow k = \sqrt {1 - {{(\cos {\varphi _2})}^2}} {\rm{}} = \sqrt {1 - 8{k^2}} {\rm{}} \Leftrightarrow {k^2} = 1 - 8{k^2} \Leftrightarrow 9{k^2} = 1 \Leftrightarrow k = \dfrac{1}{3}\)
Hướng dẫn giải:
Sử dụng giản đồ véc-tơ và biểu thức toán học