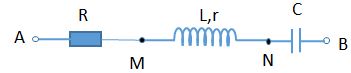
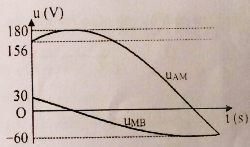
Đặt điện áp xoay chiều vào mạch điện \(AB\) gồm ba đoạn mạch nối tiếp: \(AM\) có cuộn dây thuần cảm với hệ số tự cảm \({L_1}\) ; \(MN\) có cuộn dây có hệ số tự cảm \({L_2}\); \(NB\) có tụ điện với điện dung \(C\). Biết điện áp tức thời trên \(MN\) trễ pha \(\dfrac{\pi }{6}\) so với điện áp trên \(AB\), \({U_{MN}} = {\text{ }}2{U_C}\) , \({Z_{L1}} = {\text{ }}5{Z_C}\). Hệ số công suất của đoạn mạch \(MN\) gần với giá trị nào sau đây nhất?
Trả lời bởi giáo viên
Vì điện áp tức thời trên \(MN\) trễ pha so với \({U_{AB}}\) , tức là cuộn dây có điện trở \(r\).
Nhiệm vụ của bài là đi tìm hệ số công suất của đoạn mạch \(MN\), hay là tìm \(cos{\varphi _{MN}}\).
Từ đề bài ta vẽ được giản đồ vecto như sau :
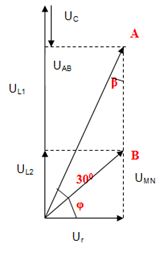
Xét tam giác \(OAB\);
Sử dụng định lí hàm số sin trong tam giác ta có:
\(\begin{array}{l}\frac{{AB}}{{\sin \left( {{{30}^0}} \right)}} = \dfrac{{OB}}{{\sin \beta }} \Leftrightarrow \dfrac{{4{U_C}}}{{0,5}} = \dfrac{{2{U_C}}}{{\sin \beta }}\\ \Rightarrow \sin \beta = \dfrac{1}{4} \Rightarrow \beta = {14^0}28'\\ \Rightarrow \varphi = {90^0} - \beta - {30^0} = {45^0}31'\\ \Rightarrow \cos \varphi \approx \dfrac{1}{{\sqrt 2 }}\end{array}\)
Hướng dẫn giải:
+ Sử dụng giản đồ véc-tơ
+ Sử dụng các hệ thức lượng trong tam giác