Câu hỏi:
2 năm trước
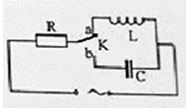
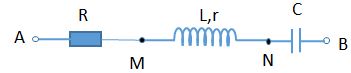
Đặt điện áp \(u = 200\sqrt 2 \cos 100\pi t\,\,\left( V \right)\) vào hai đầu đoạn mạch AB gồm đoạn mạch AM mắc nối tiếp với đoạn mạch MB, trong đó đoạn mạch AM chứa cuộn dây điện trở r = 20 Ω, đoạn mạch MB chứa điện trở thuần R = 50 Ω nối tiếp với tụ điện có điện dung C thay đổi. Khi \(C = {C_1} = \dfrac{{200}}{\pi }\,\,\mu F\) thì trong mạch xảy ra hiện tượng cộng hưởng. Điều chỉnh \(C = {C_2}\) thì \({U_{MB\max }}\), giá trị cực đại đó xấp xỉ bằng
Trả lời bởi giáo viên
Đáp án đúng: b
Mạch xảy ra cộng hưởng, ta có:
\({Z_L} = {Z_{{C_1}}} \Rightarrow {Z_L} = \dfrac{1}{{\omega {C_1}}} = \dfrac{1}{{100\pi .\dfrac{{{{200.10}^{ - 6}}}}{\pi }}} = 50\,\,\left( \Omega \right)\)
Hiệu điện thế hiệu dụng giữa hai đầu đoạn mạch MB là:
\(\begin{array}{l}{U_{MB}} = {U_{RC}} = \dfrac{{U.\sqrt {{R^2} + {Z_C}^2} }}{{\sqrt {{{\left( {R + r} \right)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\\ \Rightarrow {U_{MB}} = \dfrac{{U.\sqrt {{{50}^2} + {Z_C}^2} }}{{\sqrt {{{70}^2} + {{\left( {50 - {Z_C}} \right)}^2}} }} = \dfrac{U}{{\sqrt {1 + \dfrac{{{{70}^2} - 100{Z_C}}}{{{{50}^2} + {Z_C}^2}}} }}\end{array}\)
Đặt \({Z_C} = x;y = \dfrac{{{{70}^2} - 100{Z_C}}}{{{{50}^2} + {Z_C}^2}} = \dfrac{{{{70}^2} - 100x}}{{{{50}^2} + {x^2}}} \Rightarrow {U_{MB}} = \dfrac{U}{{\sqrt {1 + y} }}\)
Để \({U_{MB\max }} \Leftrightarrow {y_{\min }} \Leftrightarrow y' = 0\)
Ta có: \(y' = \dfrac{{ - 100.\left( {{{50}^2} + {x^2}} \right) - 2x.\left( {{{70}^2} - 100x} \right)}}{{{{\left( {{{50}^2} + {x^2}} \right)}^2}}}\)
\(\begin{array}{l}y' = 0 \Leftrightarrow - 100.\left( {{{50}^2} + {x^2}} \right) - 2x.\left( {{{70}^2} - 100x} \right) = 0\\ \Rightarrow 100{x^2} - {2.70^2}x - {100.50^2} = 0\\ \Rightarrow \left[ \begin{array}{l}x = 119\,\,\left( \Omega \right)\\x = - 21\,\,\left( {loai} \right)\end{array} \right.\\ \Rightarrow {U_{MB\max }} = \dfrac{{200.\sqrt {{{50}^2} + {{119}^2}} }}{{\sqrt {{{70}^2} + {{\left( {50 - 119} \right)}^2}} }} \approx 262,6\,\,\left( V \right)\end{array}\)
Hướng dẫn giải:
Mạch có cộng hưởng: \({Z_L} = {Z_C}\)
Hiệu điện thế hiệu dụng giữa hai đầu đoạn mạch MB: \({U_{MB}} = {U_{RC}} = \dfrac{{U.\sqrt {{R^2} + {Z_C}^2} }}{{\sqrt {{{\left( {R + r} \right)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\)
Câu hỏi khác
- Bài tập các mạch điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập mạch RLC mắc nối tiếp có lời giải MÔN LÝ lớp 12
- Bài tập pha u,i - viết phương trình u, i có lời giải MÔN LÝ lớp 12
- Bài tập lý thuyết đại cương về dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập đại cương dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
