Cho tam giác nhọn \(ABC\) nội tiếp đường tròn \(\left( O \right),\) các đường cao\(AD,\,BE,\,CF\,\left( {D \in BC,\,E \in AC,\,F \in AB} \right)\) cắt nhau tại \(H\). Khi đó ta có

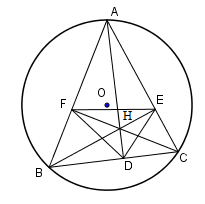
Do \(AD,\,BE\) là các đường cao nên \(\widehat {HDC} = \widehat {HEC} = {90^0}.\)

Do đó $\widehat {HDC} + \widehat {HEC} = {90^0} + {90^0} = {180^0}.$

Vậy tứ giác \(DCEH\) là tứ giác nội tiếp.

Các góc \(\widehat {HED},\,\widehat {HCD}\) cùng chắn cung \(HD\) nên

\(\widehat {HED} = \,\widehat {HCD}\,\,\left( 1 \right).\)

Xét hai tam giác \(\Delta BDE,\,\,\Delta BHC\) có \(\widehat {HED} = \,\widehat {HCD}\,\) (theo \(\left( 1 \right)\) ) và góc \(\widehat {EBC}\) chung.

Do đó \(\Delta BDE \backsim \,\Delta BHC.\) Từ đó ta nhận được \(\dfrac{{BD}}{{BH}} = \dfrac{{BE}}{{BC}} \Rightarrow BH.BE = BC.BD.\) Đáp án A đúng.

Chứng minh tương tự ta có \(\Delta CHB \backsim \Delta CDF\,\left( {g - g} \right) \Leftrightarrow \dfrac{{CH}}{{CD}} = \dfrac{{CB}}{{CF}}\) hay  \(CH.CF = CD.CB.\) Đáp án B đúng.

Vậy cả A, B đều đúng.