Cho tam giác nhọn \(ABC\,\,\left( {AB > BC} \right)\) nội tiếp đường tròn \(\left( O \right).\) \(D\) là điểm chính giữa cung \(AC.\) Giả sử \(\{E\} = AB \cap CD,\,\,\{F\} = AD \cap BC.\) Khi đó :
Trả lời bởi giáo viên
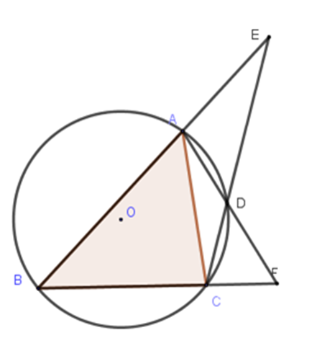
Theo tính chất của góc ngoài đường tròn ta có
\(\left\{ \begin{array}{l}\widehat {AED} = \dfrac{1}{2}\left( {sđ\,\overparen{BC} - sđ\,\overparen{AD}} \right)\\\widehat {CFD} = \dfrac{1}{2}\left( {sđ\,\overparen{AB} - sđ\,\overparen{CD}} \right)\end{array} \right.\,\,\left( 1 \right).\)
Theo đề bài ta có \(AB > BC \Rightarrow sđ\,\overparen{BC} < sđ\,\overparen{AB}\,\,\left( 2 \right).\)
Mặt khác ta có \(D\) là điểm chính giữa cung \(AC\) nên \(sđ\,\overparen{AD} = sđ\,\overparen{CD}\,\left( 3 \right).\)
Từ \(\left( 1 \right),\,\left( 2 \right)\) và \(\left( 3 \right)\) ta có \(\widehat {AED} < \widehat {CFD}.\)
Hướng dẫn giải:
Sử dụng tính chất góc có đỉnh nằm ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.


