Cho tam giác $ABC.$  Gọi $D,E,F\;$  theo thứ tự là trung điểm của $AB,BC,CA.$  Gọi $M,N,P,Q$  theo thứ tự là trung điểm của $AD,AF,EF,ED.\;$

$\Delta ABC$  có điều kiện gì thì $MNPQ$  là hình chữ nhật?

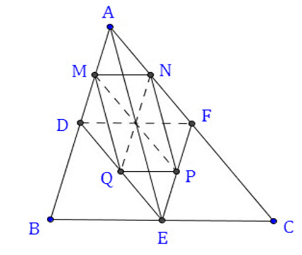
Xét $\Delta ADE$ có: $AM = DM;DQ = EQ$ nên $MQ$  là đường trung bình của $\Delta ADE$ .
$ \Rightarrow MQ//AE;MQ = \dfrac{1}{2}AE$  
Xét$\;\Delta AEF$  có: $AN = NF;FP = PE$  (giả thiết) nên $NP$ là đường trung bình của $\Delta AFE$.
$ \Rightarrow NP//AE;NP = \dfrac{1}{2}AE$

Suy ra $MQ//NP $ ( cùng $//AE$ )  và $MQ = NP(= \dfrac{1}{2}AE)$ 
Tứ giác $MNPQ$ có: $MQ//NP$  và $MQ = NP$  nên là hình bình hành (dấu hiệu nhận biết).

Để $MNPQ$ là hình chữ nhật thì $MN \bot NP$  (1)
Ta có: $NP//AE$  (chứng minh trên) (2).
Ta lại có: $AM = MD,AN = NF$  (giả thiết) 
$ \Rightarrow MN//DF$. 
Mặt khác: $AD = DB,AF = FC$  (giả thiết) 
$ \Rightarrow DF//BC$

Vậy $MN//BC$  (3)

Từ (1), (2), (3) suy ra: $AE \bot BC$ . 
Mà $BE = EC$  (giả thiết) 
Do đó $\Delta ABC$ cân tại $A$ (do \(AE\) vừa là đường cao, vừa là đường trung tuyến).