Câu hỏi:
2 năm trước
Cho Parabol \((P):y = {x^2}\) và đường thẳng \((d):y = mx + 4\) . Biết đường thẳng \((d)\) luôn cắt đồ thị \((P)\) tại hai điểm phân biệt \(A,B\) .Gọi \({x_1},{x_2}\) là hoành độ của các điểm \(A,B.\)
Tìm \(m\) để diện tích tam giác \(OAB\) bằng \(8\) .
Trả lời bởi giáo viên
Đáp án đúng: a
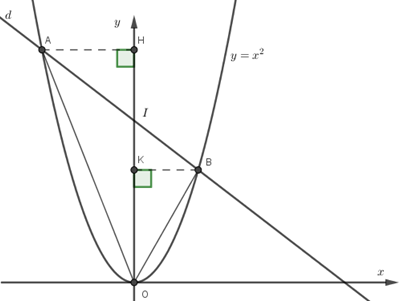
Để ý rằng đường thẳng \(\left( d \right)\) luôn đi qua điểm cố định \(I\left( {0;4} \right)\) nằm trên trục tung. Ngoài ra nếu gọi $A\left( {{x_1};{y_1}} \right),B\left( {{x_2};{y_2}} \right)$ thì \({x_1}.{x_2} = - 4 < 0\)
(do \({x_1};{x_2}\) là hai nghiệm của phương trình hoành độ giao điểm \({x^2} - mx - 4 = 0\) )
nên hai giao điểm $A,B$ nằm về hai phía trục tung.
Giả sử \({x_1} < 0 < {x_2}\) thì ta có:
\({S_{OAB}} = {S_{OAI}} + {S_{OBI}} = \dfrac{1}{2}AH.OI + \dfrac{1}{2}BK.OI\) với \(H,K\) lần lượt là hình chiếu vuông góc của điểm \(A,B\) trên trục \(Oy\). Ta có \(OI = 4,AH = \left| {{x_1}} \right| = - {x_1},BK = \left| {{x_2}} \right| = {x_2}\). Suy ra \({S_{OAB}} = 2\left( {{x_2} - {x_1}} \right)\) \( \Rightarrow S_{OAB}^2 = 4{\left( {{x_1} - {x_2}} \right)^2} = 4\left[ {{{\left( {{x_1} + {x_2}} \right)}^2} - 4{x_1}{x_2}} \right]\).
Theo định lý Viet ta có: \({x_1} + {x_2} = m,{x_1}{x_2} = - 4\). Thay vào ta có: $S_{OAB}^2 = 4\left( {{m^2} + 16} \right) = 64 \Leftrightarrow m = 0$.
Hướng dẫn giải:
+ Kẻ \(H,K\) lần lượt là hình chiếu vuông góc của điểm \(A,B\) trên trục \(Oy\)
+ \({S_{OAB}} = {S_{OAI}} + {S_{OBI}} = \dfrac{1}{2}AH.OI + \dfrac{1}{2}BK.OI\)
Giải thích thêm:
Nếu thay điều kiện \(S = 8\) thành diện tích tam giác \(OAB\) nhỏ nhất ta cũng có kết quả như trên.
Vì \({m^2} \ge 0 \Rightarrow {S^2} \ge 4\left( {{m^2} + 16} \right) \ge 64\).
Câu hỏi khác
- Bài tập hàm số bậc hai một ẩn và đồ thị hàm số y=ax^2 toán 9 có lời giải
- Bài tập hệ thức vi-ét và ứng dụng toán 9 có lời giải
- Bài tập phương trình bậc hai một ẩn và công thức nghiệm toán 9 có lời giải
- Bài tập công thức nghiệm thu gọn toán 9 có lời giải
- Bài tập phương trình quy về phương trình bậc hai toán 9 có lời giải
