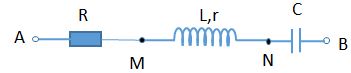
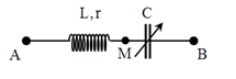
Cho mạch điện như hình vẽ. Đặt vào hai đầu A,B một điện áp xoay chiều có giá trị hiệu dụng U và tần số f không đổi. Điều chỉnh C để tổng điện áp hiệu dụng UAM+ UMB lớn nhất thì tổng đó bằng 2U và khi đó công suất tiêu thụ của đoạn mạch AM là 36W. Tiếp tục điều chỉnh C để công suất tiêu thụ của đoạn mạch lớn nhất thì công suất lớn nhất đó bằng:
Trả lời bởi giáo viên
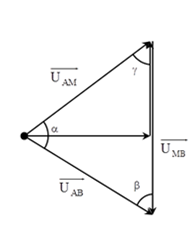
+ Áp dụng định lý sin trong tam giác, ta có: UAMsinβ=UMBsinα=UABsinγ→UAM+UMB=UMBsinγ(sinα+sinβ)
với γ luôn không đổi.
Biến đổi lượng giác UAM+UMB=2UABsinγsin(180−γ2)cos(α−β2)
+ Khi đó: (UAM+UMB)max
Các vecto hợp với nhau thành tam giác đều => khi xảy ra cực đại u chậm pha hơn i một góc {30^0}.
P = {P_{\max }}{\cos ^2}\varphi {\text{}} \to {P_{\max }} = \dfrac{P}{{{{\cos }^2}\varphi }} = \dfrac{{36}}{{{{\cos }^2}{{30}^\circ }}} = 48{\mkern 1mu} {\mkern 1mu} W.
Hướng dẫn giải:
Áp dụng phương pháp giản đồ vectơ trong mạch điện xoay chiều