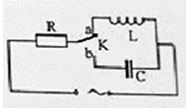
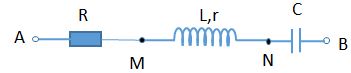
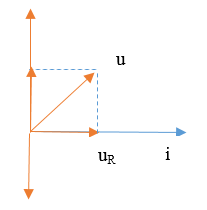
Cho mạch điện như hình vẽ bên. Cuộn dây thuần cảm. Tụ điện có điện dung C biến đổi. Đặt vào hai đầu đoạn mạch một điện áp \(u = U\sqrt 2 .\cos \left( {\omega t + \varphi } \right)\) (trong đó U, ɷ, φ không đổi). Khi C = C1biểu thức của điện áp hai đầu R là \({u_{AM}} = 126.\cos \left( {\omega t - \frac{\pi }{4}} \right)V\). Khi C = C2biểu thức của điện áp hai đầu R là \({u_{AM}} = 77.\cos \left( {\omega t + \frac{\pi }{3}} \right)V\). Điện áp U gần nhất với giá trị nào sau đây?
Trả lời bởi giáo viên
Đề bài cho điện áp uAM chính là điện áp hai đầu R, vì uR cùng pha với cường độ dòng điện i, nên ta có giản đồ vecto khi C = C1 là:
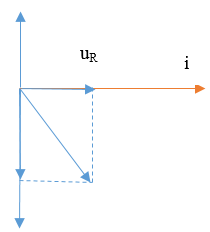
Khi C = C2 ta có
Độ lệch pha của cường độ dòng điện trong hai lần là:
\(\Delta {\varphi _{\left( {{i_1};{i_2}} \right)}} = \frac{\pi }{4} + \frac{\pi }{3} = \frac{{7\pi }}{{12}}\)
Ta có:
\(\begin{array}{l}
\left\{ \begin{array}{l}
\cos {\varphi _1} = \frac{{{U_{R1}}}}{U} \Rightarrow {\varphi _1} = {\rm{arc}}\cos \frac{{{U_{R1}}}}{U}\\
\cos {\varphi _2} = \frac{{{U_{R2}}}}{U} \Rightarrow {\varphi _2} = {\rm{arc}}\cos \frac{{{U_{R2}}}}{U}
\end{array} \right.\\
\Rightarrow \arccos \frac{{{U_{R1}}}}{U} + \arccos \frac{{{U_{R2}}}}{U} = \frac{{7\pi }}{{12}}
\end{array}\)
Thay số và bấm máy tính tìm U:
\(\arccos \frac{{126}}{{\sqrt 2 U}} + {\rm{ar}}\cos \frac{{77}}{{\sqrt 2 U}} = \frac{{7\pi }}{{12}}\)
Ta được
\(U = 119,9V \approx 120V\)
Vậy U gần nhất với giá trị 115V.
Hướng dẫn giải:
Áp dụng giản đồ vecto và sử dụng góc lệch pha giữa u và i.