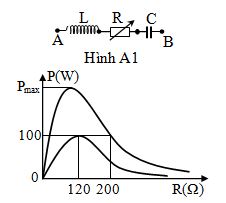
Cho mạch điện như hình A1, cuộn dây thuần cảm. Điện áp hai đầu đoạn mạch có biểu thức với $U$ không đổi nhưng $f$ có thể thay đổi được. Ta có đồ thị biểu diễn sự phụ thuộc của công suất tiêu thụ trên mạch theo $R$ là đường liền nét khi $f = {f_1}$ và là đường đứt nét khi $f = {f_2}$ . Giá trị của ${P_{max}}$  gần nhất với giá trị nào sau đây?

Đặt điện áp $u = 180\sqrt 2 {\rm{cos}}\omega {\rm{t (V)}}$ (với $\omega$ không đổi) vào hai đầu đoạn mạch AB gồm đoạn mạch AM  nối tiếp đoạn mạch MB. Đoạn mạch AM có điện trở thuần R, đoạn mạch MB có cuộn cảm thuần có độ tự cảm L thay đổi được và tụ điện có điện dung C mắc nối tiếp. Điện áp hiệu dụng ở hai đầu đoạn mạch AM và độ lớn góc lệch pha của cường độ dòng điện so với điện áp u khi $L = {L_1}$  là $U$ và ${\varphi _1}$, còn khi $L = {L_2}$  thì tương ứng là $\sqrt 8 U$ và ${\varphi _2}$ . Biết ${\varphi _1} + {\varphi _2} = {90^0}$. Hệ số công suất của mạch khi $L = {L_1}$  là:

Điện năng được truyền từ nơi phát đến một khu dân cư bằng đường dây một pha với hiệu suất truyền tải là $75\%$. Coi hao phí điện năng chỉ do tỏa nhiệt trên đường dây và không vượt quá $40\%$. Nếu công suất sử dụng điện của khu dân cư này tăng $25\%$ và giữ nguyên điện áp ở nơi phát thì hiệu suất truyền tải điện năng trên chính đường dây đó là:

Cho dòng điện xoay chiều  chạy qua  đoạn mạch AB có sơ đồ  như hình bên, trong đó L là cuộn cảm thuần và X là đoạn mạch xoay chiều. Khi đó, điện áp giữa hai đầu các đoạn mạch AN và MB có biểu thức  lần lượt ${u_{AN}} = 30\sqrt 2 cos\omega t(V);{u_{MB}} = 40\sqrt 2 cos\left( {\omega t - \frac{{\pi {\rm{}}}}{2}} \right)(V)$

Điện áp hiệu dụng giữa hai đầu đoạn mạch AB có giá trị nhỏ nhất là:

Đặt điện áp xoay chiều $u = {U_0}cos\left( {\omega t + \varphi } \right)$ vào  hai đầu đoạn mạch AB gồm điện trở , tụ  điện và cuộn cảm thuần mắc nối tiếp  (hình ${H_1}$ ).  Ban đầu  khóa K đóng, sau đó khóa K mở. Hình ${H_2}$  là  đồ thị biểu diễn sự  phụ thuộc của cường  độ dòng  điện i trong  đoạn mạch vào thời gian t. Giá trị  của ${U_0}$ gần nhất với giá trị nào sau đây?

Đặt điện áp $u = {U_0}{\rm{cos100}}\pi {\rm{t}}\left( V \right)$ (t tính bằng s) vào đoạn mạch gồm cuộn dây và tụ điện mắc nối tiếp. Cuộn dây có độ tự cảm $L = \frac{{1,5}}{\pi }H$, điện trở $r = 50\sqrt 3 \Omega$, tụ điện có điện dung $C = \frac{{{{10}^{ - 4}}}}{\pi }F$ . Tại thời điểm ${t_1}$, điện áp tức thời giữa hai đầu cuộn dây có giá trị $150V$, đến thời điểm ${t_1} + \frac{1}{{75}}s$ thì điện áp giữa hai đầu tụ điện cũng bằng $150V$. Giá trị của ${U_0}$ bằng:

Cho mạch điện xoay chiều gồm điện trở thuần R, tụ điện có điện dung C và cuộn dây có độ tự cảm L mắc nối tiếp theo thứ tự đó. Biết tụ điện có điện dung C có thể thay đổi được, khi $C = {C_1} = \dfrac{{62,5}}{\pi }\mu F$ điện áp hai đầu mạch $U = 150V$ thì mạch tiêu thụ công suất cực đại ${P_{max}} = 93,75{\rm{ }}W$. Khi $C = {C_1} = \dfrac{1}{{9\pi }}\mu F$  thì điện áp hiệu dụng trên hai đầu đoạn mạch chứa điện trở thuần và tụ điện $\left( {{u_{RC}}} \right)$ và cuộn dây $\left( {{u_d}} \right)$ vuông pha với nhau, điện áp hiệu dụng hai đầu cuộn dây khi đó là:

Điện năng được truyền từ nơi phát đến một xưởng sản xuất bằng đường dây một pha với hiệu suất truyền tải là $90\%$. Ban đầu xưởng sản xuất này có $90$ máy hoạt động, vì muốn mở rộng quy mô sản xuất nên xưởng đã nhập thêm về một số máy. Hiệu suất truyền tải lúc sau (khi có thêm các máy mới cùng hoạt động) đã giảm đi $10\%$ so với ban đầu. Coi hao phí điện năng chỉ do toả nhiệt trên đường dây, công suất tiêu thụ điện của các máy hoạt động (kể cả các máy mới nhập về) đều như nhau và hệ số công suất trong các trường hợp đều bằng $1$. Nếu giữ nguyên điện áp nơi phát thì số máy hoạt động đã được nhập về thêm là: