Câu hỏi:
2 năm trước
Cho hình vuông\(ABCD\) cạnh \(8\,cm\). \(M,N,P,Q\) là trung điểm các cạnh\(AB,BC,CD,DA\). Tính diện tích tứ giác \(MNPQ.\)
Trả lời bởi giáo viên
Đáp án đúng: d
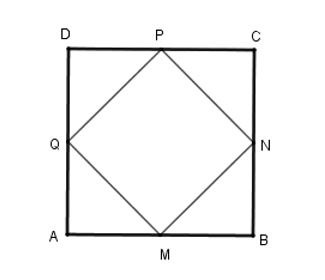
Vì \(ABCD\) là hình vuông và \(M,N,P,Q\) là trung điểm các cạnh\(AB,BC,CD,CA\) nên ta có \(AM = MB = BN = NC = CP = PD = DQ = QA = \dfrac{8}{2} = 4cm\).
Từ đó \(\Delta AQM = \Delta BMN = \Delta CPN = \Delta DQP\,\left( {c - g - c} \right)\).
Suy ra: \({S_{QAM}} = {S_{MNB}} = {S_{CPN}} = {S_{DPQ}} = \dfrac{{DQ.QP}}{2} = \dfrac{{{8^2}}}{8} = 8\).
Lại có: \({S_{ABCD}} = {8^2} = 64\).
Nên \({S_{MNPQ}} = {S_{ABCD}} - {S_{AMQ}} - {S_{MBN}} - {S_{CPN}} - {S_{DPQ}}\)\( = {8^2} - 4. \dfrac{{{8^2}}}{8} = \dfrac{1}{2}{.8^2} = 32\).
Vậy \({S_{MNPQ}} = 32\,c{m^2}\).
Hướng dẫn giải:
Sử dụng công thức tính diện tích tam giác và công thức tính diện tích hình vuông để tính diện tích \(MNPQ\).
