Tứ giác $AKMB$ là hình gì?

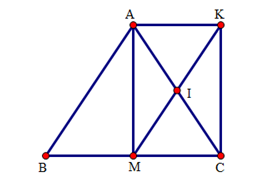
+ Tam giác $ABC$ cân tại$A$ , $AM$ là đường trung tuyến nên $AM$ đồng thời là đường cao.

$\Rightarrow AM \bot BC \Rightarrow \widehat {AMC} = 90^\circ$

Xét tứ giác $AMCK$ có:

$\left\{ \begin{array}{l}AI = IC(gt)\\MI = IK(gt)\\AC \cap MK = I\,(gt)\end{array} \right.$

Suy ra tứ giác $AMCK$ là hình bình hành (dhnb).

Lại có: $\widehat {AMC} = 90^\circ (cmt)$ nên hình bình hành $AMCK$ là hình chữ nhật.

+ Ta có:

$AK{\rm{//}}MC$ ( do $AMCK$ là hình chữ nhật), $M \in BC(gt) \Rightarrow AK{\rm{//}}BM$

Mà $BM = MC$ ( do $AM$ là trung tuyến), $AK = MC$ (do $AMCK$ là hình chữ nhật)  nên $AK = BM$ (tính chất bắc cầu)

Xét tứ giác $ABMK$ có:

$\left\{ \begin{array}{l}AK = BM(cmt)\\AK{\rm{//}}BM(cmt)\end{array} \right.$

Suy ra tứ giác $ABMK$ là hình bình hành.