Tứ giác $EFGH$ là hình gì?

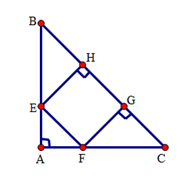
Ta có: $\Delta ABC$ vuông cân tại $A$ nên $\widehat B = \widehat C = \dfrac{{180^\circ  - \widehat A}}{2} = \dfrac{{180^\circ  - 90^\circ }}{2} = 45^\circ$ 

Xét tam giác vuông $FGC$ có

 $\widehat {GFC} = 180^\circ  - \widehat {FGC} - \widehat C = 180^\circ  - 90^\circ  - 45^\circ  = 45^\circ$ $\Rightarrow \widehat {GFC} = \widehat C$

Suy ra $\Delta FGC$ là tam giác vuông cân tại $G$ $\Rightarrow FG = GC$

Chứng minh tương tự:

Xét tam giác vuông $EHB$ có

 $\widehat {BEH} = 180^\circ  - \widehat {EHB} - \widehat B = 180^\circ  - 90^\circ  - 45^\circ  = 45^\circ$$\Rightarrow \widehat {BEH} = \widehat B$

Suy ra tam giác $EBH$ vuông cân tại $H$ $\Rightarrow EH = HB$

Mà $BH = HG = GC(gt)$ nên $FG = EH = HG$

Lại có: $\left. \begin{array}{l}EH \bot BC(gt)\\FG \bot BC(gt)\end{array} \right\} \Rightarrow EH{\rm{//}}FG$ ( định lí từ vuông góc đến song song)

Xét tứ giác $EFGH$ có:

$\left\{ \begin{array}{l}EH = FG(cmt)\\EH{\rm{//}}FG(cmt)\end{array} \right.$ $\Rightarrow$ Tứ giác $EFGH$ là hình bình hành (dhnb)

Mà $\widehat H = 90^\circ$ ( do $EH \bot BC$ ) nên hình bình hành $EFGH$ là hình chữ nhật.

Mặt khác $EH = HG(cmt)$ nên hình chữ nhật $EFGH$ là hình vuông.