Cho hình vẽ (hai đường tròn có tâm là \(B,C \) và điểm \(B\) nằm trên đường tròn tâm \(C\)). Biết $\widehat {MAN} = {20^0}.$
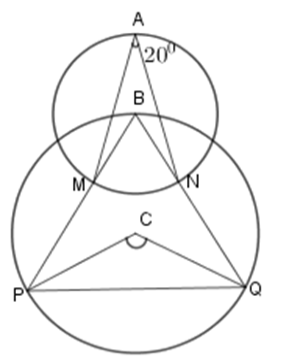
Khi đó \(\widehat {PCQ} = ?\)
Trả lời bởi giáo viên
Ta nhận thấy \(\widehat {MAN}\) nội tiếp đường tròn tâm \(B\), chắn cung nhỏ \(MN\) của đường tròn \(\left( B \right)\) nên \(\widehat {MAN} = \dfrac{1}{2}\widehat {MBN} = {20^0} \Rightarrow \widehat {MBN} = {40^0} \Rightarrow \widehat {PBQ} = {40^0}.\)
Ta lại có \(\widehat {PBQ}\) là góc nội tiếp đường tròn tâm \(C\) và \(\widehat {PCQ}\) là góc ở tâm của \(\left( C \right)\) nên
$\widehat {PBQ} = \dfrac{1}{2}\widehat {PCQ} \Rightarrow \widehat {PCQ} = 2\widehat {PBQ} = {80^0}.$
Vậy \(\widehat {PCQ} = {80^0}.\)
Hướng dẫn giải:
Sử dụng tính chất góc nội tiếp và góc ở tâm
Số đo của góc nội tiếp bằng nửa số đo cung bị chắn
Số đo góc ở tâm bằng số đo cung bị chắn


