Trả lời bởi giáo viên
Đáp án đúng: d
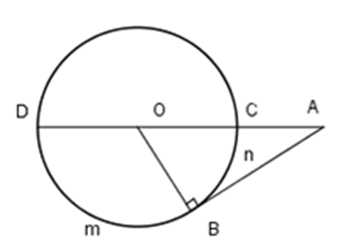
Xét $(O)$ có $\widehat {BOD} = sđ \overparen{BmD}=120^0$
mà góc $BOD$ và $AOB$ là hai góc kề bù nên \(\widehat {AOB} = 180^\circ - \widehat {BOD} = 60^\circ \)
Xét tam giác $AOB$ vuông tại $B$ (do $AB$ là tiếp tuyến) nên
\( \widehat {AOB} + \widehat {OAB} = 90^\circ \Rightarrow \widehat {OAB} = 90^\circ - 60^\circ = 30^\circ \)
Hướng dẫn giải:
Tính góc $BOD$ rồi suy ra góc $BOA$
Từ đó ta tính được góc $OAB$