Cho hình thoi \(ABCD,O\) là giao điểm của hai đường chéo. Các tia phân giác 4 góc đỉnh \(O\) cắt các cạnh \(AB,BC,CD,DA\) theo thứ tự ở \(E,F,G,H.\) Tứ giác \(EFGH\) là hình gì?

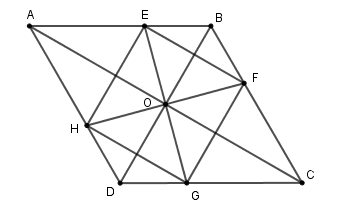
+ Vì \(ABCD\) là hình thoi nên \(AC \bot BD; \,OA = OC; OB = OD\) (tính chất).

Mà \(OE;OF;OG;OH\) lần lượt là phân giác \(\widehat {AOB};\,\widehat {BOC};\,\widehat {DOG};\,\widehat {AOD}\)  nên ta có \(\widehat {EOB} = \widehat {OHA} = \widehat {BOF} = 45^\circ \).

Suy ra: \(\widehat {HOA} + \widehat {AOB} + \widehat {BOF} = 45^\circ  + 90^\circ  + 45^\circ  = 180^\circ \) nên \(H,O,F\) thẳng hàng.

Tương tự ta có: \(E,O,G\) thẳng hàng.

Xét \(\Delta OEB\) và \(\Delta OGD\) ta có \(OD = OB;\,\widehat {EOB} = \widehat {GOD}\) (đối đỉnh); \(\widehat {EBO} = \widehat {ODG}\) (so le trong) nên \(\Delta OEB = \Delta OGD\left( {g - c - g} \right)\) suy ra \(OE = OG\)  (1)

Tương tự ta có: \(\Delta OFB = \Delta OHD\left( {g - c - g} \right) \Rightarrow OF = OH\) (2)

Từ (1) và (2) suy ra: tứ giác \(EFGH\) là hình bình hành vì có hai đường chéo \(EG;HF\) giao nhau tại trung ddierm mỗi đường.

Lại xét \(\Delta OEB\) và \(\Delta OFB\) có:

+ \(\widehat {EBO} = \widehat {FBO}\)  (do \(BO\) là phân giác \(\widehat {ABC}\))

+ Cạnh \(OB\) chung

+ \(\widehat {EOB} = \widehat {BOF} = 45^\circ \)

Nên \(\Delta OEB = \Delta OFB\left( {g - c - g} \right) \Rightarrow OE = OF \Rightarrow 2OE = 2OF\) hay \(EG = HF\).

Suy ra: hình bình hành \(EFGH\) có hai đường chéo bằng nhau \(EG = HF\) nên \(EFGH\) là hình chữ nhật.

Lại có: \(\widehat {EOB} + \widehat {BOF} = 45^\circ  + 45^\circ  = 90^\circ \)\( \Rightarrow \widehat {EOF} = 90^\circ  \Rightarrow EG \bot FH\).

Hình chữ nhật \(EFGH\) có: \(EG \bot HF\) nên \(EFGH\) là hình vuông.