Câu hỏi:
2 năm trước
Cho hình bình hành \(ABEF\). Gọi \(O\) là giao điểm của \(AE\) và \(BF\). Trong các khẳng định sau:
1. \(E\) và \(A\) đối xứng nhau qua \(O\).
2. \(B\) và \(F\) đối xứng nhau qua \(O\).
3. \(E\) và \(F\) đối xứng nhau qua \(O\).
4. \(AB\) và $EF$ đối xứng nhau qua \(O\).
Có bao nhiêu khẳng định đúng ?
Trả lời bởi giáo viên
Đáp án đúng: c
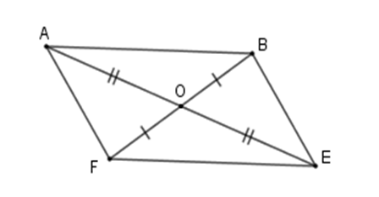
Hình bình hành \(ABCD\) có \(OA = OE;\,OB = OF\) nên
+ \(E\) và \(A\) đối xứng nhau qua \(O\).
+ \(B\) và \(F\) đối xứng nhau qua \(O\).
+ \(AB\) và $EF$ đối xứng nhau qua \(O\).
Nhưng \(E\) và \(F\) không đối xứng nhau qua \(O\) vì \(OE \ne OF;\,O\) không thuộc \(EF\) .
Vậy có \(3\) khẳng định đúng.