Câu hỏi:
2 năm trước
Cho hàm số $y = \dfrac{{ax - 1}}{{x + d}}$ có bảng biến thiên
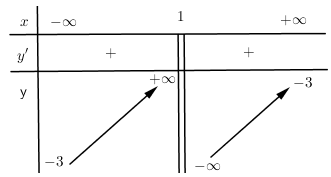
Giá trị của ${a^2} + {d^2}$ bằng:
Trả lời bởi giáo viên
Đáp án đúng: d
Xét hàm số $y = \dfrac{{ax - 1}}{{x + d}}$
+) Tiệm cận đứng $x = - d$ mà theo bảng biến thiên tiệm cận đứng của đồ thị hàm số là \(x = 1\) suy ra $d = - 1$.
+) Tiệm cận ngang $y = \dfrac{a}{1}$ mà theo bảng biến thiên tiệm cận ngang của đồ thị hàm số là $y = - 3$ suy ra $a = - 3$.
Vậy: ${a^2} + {d^2} = {\left( { - 3} \right)^2} + {\left( { - 1} \right)^2} = 10$
Hướng dẫn giải:
- Quan sát bảng biến thiên, tìm các đường tiệm cận đứng, ngang của đồ thị hàm số.
- Tìm $a,d \Rightarrow {a^2} + {d^2}$.
Câu hỏi khác
- Bài tập sự đồng biến, nghịch biến của hàm số toán 12 có lời giải
- Bài tập cực trị của hàm số toán 12 có lời giải
- Bài tập giá trị lớn nhất và giá trị nhỏ nhất của hàm số toán 12 có lời giải
- Bài tập cực trị có tham số đối với các hàm số cơ bản môn Toán lớp 12
- Bài tập đồ thị của hàm số và phép tịnh tiến hệ tọa độ toán 12 có lời giải
