Cho hàm số \(y = \dfrac{{2x + 1}}{{x + 1}}(C)\), gọi \(I\) là tâm đối xứng của đồ thị \((C)\) và \(M(a;b)\) là một điểm thuộc đồ thị. Tiếp tuyến của đồ thị \((C)\) tại điểm \(M\) cắt hai tiệm cận của đồ thị \((C)\) lần lượt tại hai điểm \(A\) và \(B\). Để tam giác $I A B$ có bán kính đường tròn nội tiếp lớn nhất thì tổng \(a + b\) bằng

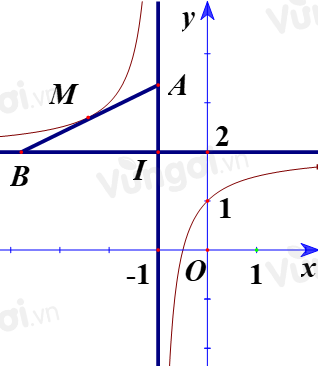
Bước 1: Tìm I và tham số hóa điểm M. Viết phương trình tiếp tuyến tại M.

Ta có \(I( - 1;2);M\left( {a;\dfrac{{2a + 1}}{{a + 1}}} \right)\). Lại có, \(y'\left( a \right) = \dfrac{1}{{{{(a + 1)}^2}}}\).

Phương trình tiếp tuyến tại \(M:y = \dfrac{1}{{{{(a + 1)}^2}}}(x - a) + \dfrac{{2a + 1}}{{a + 1}}\).

Bước 2: Tìm giao của tiếp tuyến với 2 đường tiệm cận.

Giao của tiếp tuyến và tiệm cận đứng \(A\left( { - 1;\dfrac{{2a}}{{a + 1}}} \right)\).

Giao của tiếp tuyến và tiệm cận ngang \(B(2a + 1;2)\).

Tam giác IAB vuông tại I.

Bước 3: Sử dụng công thức diện tích để chứng minh tích p.r là một hằng số không đổi.

Ta có \(IA = \dfrac{2}{{|a + 1|}};IB = 2|a + 1|\);

\({S_{\Delta IAB}} = \dfrac{1}{2}IA.IB = 2\).

Mà \({S_{\Delta IAB}} = p.r \Rightarrow p.r = 2\)

\(p = IA + IB + AB\)\( = IA + IB + \sqrt {I{A^2} + I{B^2}} \)\( \ge 2\sqrt {IA.IB}  + \sqrt {2.IA.IB} \)\( = 2\sqrt {2.4}  + \sqrt {2.2.4} =4+4\sqrt {2}\)

Bước 4: Lập luận tìm a+b.

Suy ra \({r_{\max }}\) khi \({p_{\min }}\). Dấu "=" xảy ra khi và chỉ khi \(IA = IB\).

Suy ra \(M\) là giao điểm của đường thẳng \(d\) đi qua \(I\) có hệ số góc \(k = - 1\) và đồ thị hàm số.

Phương trình \(d\) có dạng \(y - 2 =  - 1(x + 1) \Leftrightarrow y =  - x + 1\)

Hoành độ giao điểm của \(d\) và đồ thị hàm số là nghiệm của phương trình \( - x +1= \dfrac{{2x + 1}}{{x + 1}} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x =  - 2}\end{array}} \right.\)

\( \Rightarrow \left[ {\begin{array}{*{20}{l}}{M(0;1)}\\{M( - 2;3)}\end{array} \Rightarrow a + b = 1} \right.\)

Vậy với cả 2 trường hợp thì giá trị của a+b đều bằng 1.