Câu hỏi:
2 năm trước
Cho hai đường tròn \(\left( {O;R} \right)\) và \(\left( {O';R'} \right)\) cắt nhau tại \(A\) và \(B.\) Vẽ cát tuyến \(CAD\) vuông góc với \(AB\left( {C \in \left( O \right),D \in \left( {O'} \right)} \right)\) . Tia \(CB\) cắt \(\left( {O'} \right)\) tại \(E,\) tia \(DB\) cắt \(\left( O \right)\) tại \(F.\) Khi đó
Trả lời bởi giáo viên
Đáp án đúng: c
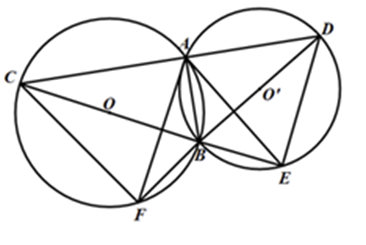
Theo giả thiết ta có \(CD \bot AB\) nên \(\widehat {CAB} = {90^0}.\) Mà \(\widehat {CAB} = \dfrac{1}{2}sđ\overparen{BC} \Rightarrow sđ \overparen{BC} = {180^0}.\)
Vậy ba điểm \(B,\,O,\,C\) thẳng hàng.
Chứng minh tương tự ta nhận được \(B,\,\,O',\,D\) thẳng hàng.
Trong \(\left( O \right)\) các góc \(\widehat {CAF},\,\widehat {CBF}\) là các góc nội tiếp cùng chắn chung \(CF\) nên $\widehat {CAF} = \,\widehat {CBF}.\,\left( 1 \right)$
Trong \(\left( {O'} \right)\) các góc \(\widehat {DAE},\,\widehat {DBE}\) là các góc nội tiếp cùng chắn chung \(DE\) nên \(\widehat {DAE} = \widehat {DBE}\,\left( 2 \right).\)
Mặt khác \(\widehat {CBF},{\kern 1pt} \widehat {DBE}\) là các góc đối đỉnh, do đó \(\widehat {CBF} = \widehat {DBE}\,\,\left( 3 \right).\)
Từ \(\left( 1 \right),\,\left( 2 \right),\,\left( 3 \right)\) ta suy ra \(\widehat {CAF} = \widehat {DAE}.\)
Hướng dẫn giải:
Sử dụng tính chất các góc nội tiếp cùng chắn một cung thì bằng nhau
