Câu hỏi:
2 năm trước
Cho góc $\widehat {xOy}\,\left( {0 < \widehat {xOy} < 180^\circ } \right)$. Đường tròn $\left( I \right)$ là đường tròn tiếp xúc với cả hai cạnh $Ox;Oy$. Khi đó điểm $I$ chạy trên đường nào?
Trả lời bởi giáo viên
Đáp án đúng: d
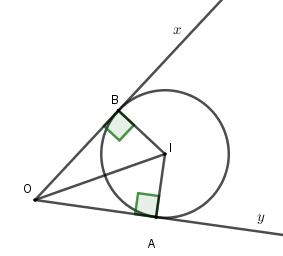
Kẻ $IA \bot Oy;IB \bot Ox$ tại $A,B$.
Vì $\left( I \right)$ tiếp xúc với cả $Ox;Oy$ nên $IA = IB$ suy ra $I$ thuộc tia phân giác của góc $\widehat {xOy}$ ($I \ne O$)
(tính chất tia phân giác của một góc)
Hướng dẫn giải:
Xác định xem tâm đường tròn cách đường thẳng cho trước một khoảng bằng bao nhiêu rồi sử dụng tính chất tia phân giác của một góc để xác định tập hợp điểm.


