Câu hỏi:
3 năm trước
Cho đường tròn tâm \(O,\) đường kính \(AB.\) Lấy điểm \(P\) khác \(A\) và \(B\) trên đường tròn sao cho \(\widehat {BAP} = {30^0}.\) Gọi \(T\) là giao điểm của \(AP\) với tiếp tuyến tại \(B\) của đường tròn. Khi đó ta có \(\widehat {PBT} = ?\)
Trả lời bởi giáo viên
Đáp án đúng: a
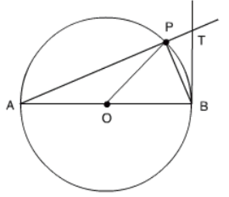
Xét $(O)$ có góc $PAB$ là góc nội tiếp chắn cung $BP$, góc $PBT$ là góc tạo bởi tia tiếp tuyến và dây cung $BP$
nên \(\widehat {PBT} = \widehat {PAB} = 30^\circ \)
Hướng dẫn giải:
Sử dụng tính chất góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn một cung thì bằng nhau.


