Cho đường tròn \(\left( {O;R} \right)\) và một điểm \(M\) bên trong đường tròn đó. Qua \(M\) kẻ hai dây cung \(AB\) và \(CD\) vuông góc với nhau (\(C\) thuộc cung nhỏ \(AB\)). Vẽ đường kính \(DE.\) Khi đó tứ giác \(ABEC\) là:
Trả lời bởi giáo viên
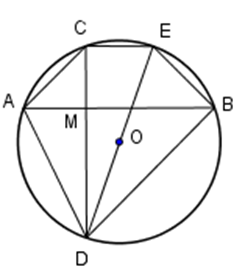
Do \(DE\) là đường kính của \(\left( {O;R} \right)\) nên \(\widehat {DCE} = {90^0}\) (góc nội tiếp chắn nửa đường tròn).
Do đó \(CD \bot CE.\) Mặt khác theo giả thiết ta có \(CD \bot AB.\)
Do đó \(AB//CE.\) Vậy tứ giác \(ABEC\) là hình thang \(\left( 1 \right).\)
Mặt khác các dây \(CE,AB\) là hai dây song song của \(\left( O \right)\) chắn hai cung \(AC\) và \(BE\) nên
Cung \(AC = \) cung \(BE \) \( \Rightarrow AC=BE\,\,\,\left( 2 \right).\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra tứ giác \(ABEC\) là hình thang cân.
Hướng dẫn giải:
Sử dụng tính chất góc nội tiếp chắn nửa đường tròn
Sử dụng dấu hiệu nhận biết các hình đặc biệt


