Cho điểm \(M\) thuộc đoạn thẳng \(AB\). Vẽ về một phía của \(AB\) các tam giác đều \(AMC\) và \(MBD\) . Gọi \(E\) là giao điểm của \(AD\) và \(MC\), \(F\) là giao điểm của \(BC\) và \(DM\) .
Tam giác \(MEF\) là tam giác gì? Chọn đáp án đúng nhất.
Trả lời bởi giáo viên
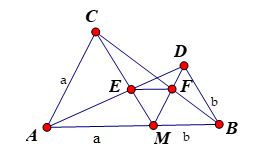
Từ câu trước ta có \(ME = MF \Rightarrow \Delta EMF \) cân tại \(M\) .
Ta có \(\widehat {AMC} + \widehat {EMF} + \widehat {DMB} = 180^\circ \) mà \(\widehat {AMC} = \widehat {DMB} = 60^\circ \) (tính chất tam giác đều), nên
\(\begin{array}{l}\widehat {EMF} = 180^\circ - \widehat {CMA} - \widehat {DMB}\\ = 180^\circ - 60^\circ - 60^\circ = 60^\circ \end{array}\)
Từ đó \(MEF\) là tam giác cân có một góc bằng \(60^\circ \) nên nó là tam giác đều.
Hướng dẫn giải:
Sử dụng kết quả câu trước $ME=MF$
Chứng minh tam giác \(MEF\) là tam giác cân có một góc bằng \(60^\circ \) .