Trả lời bởi giáo viên
Đáp án đúng: b
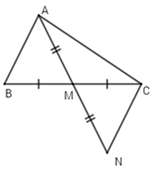
Trên tia đối của tia $MA$ lấy điểm $N$ sao cho $MN = MA.$
Vì $M$ là trung điểm của $BC$ (gt) \( \Rightarrow MB = MC\) (tính chất trung điểm)
Xét \(\Delta MAB\) và \(\Delta MNC\) có:
\(MB = MC\left( {cmt} \right)\)
\(\widehat {AMB} = \widehat {NMC}\) (đối đỉnh)
\(AM = MN\left( {gt} \right)\)
\( \Rightarrow \Delta MAB = \Delta MNC\left( {c - g - c} \right)\) \( \Rightarrow NC = AB\left( 1 \right)\) (2 cạnh tương ứng)
Xét \(\Delta ACN\) có: \(AN < AC + CN\left( 2 \right)\) (bất đẳng thức tam giác)
Từ \(\left( 1 \right)\left( 2 \right) \Rightarrow AN < AC + AB\).
Mặt khác, \(AN = 2AM\left( {gt} \right) \Rightarrow 2AM < AB + AC.\)
Hướng dẫn giải:
- Kẻ thêm hình: Trên tia đối của tia $MA$ lấy điểm $N$ sao cho $MN = MA.$
- Áp dụng bất đẳng thức tam giác: Trong một tam giác, tổng độ dài hai cạnh bất kì lớn hơn độ dài cạnh còn lại.
Câu hỏi khác
- Bài tập mối quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu toán 7 có lời giải
- Bài tập về ba đường trung tuyến của tam giác toán 7 có lời giải
- Bài tập quan hệ giữa góc và cạnh đối diện trong một tam giác toán 7 có lời giải
- Bài tập quan hệ giữa ba cạnh của một tam giác toán 7 có lời giải
- Bài tập về ba đường phân giác của tam giác toán 7 có lời giải
