Câu hỏi:
2 năm trước
Cho \(BC = R\sqrt 3 .\)Tính theo $R$ độ dài cung nhỏ $BC$ của đường tròn (O; R).
Trả lời bởi giáo viên
Đáp án đúng: a
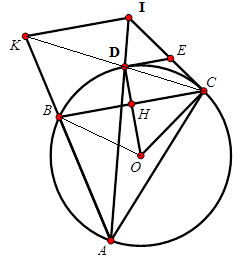
Gọi \(OD \cap BC\) tại \(H\) thì \(H\) là trung điểm \(BC\) (do \(OD \bot BC\) tại \(H\) )\( \Rightarrow HC = \dfrac{{BC}}{2} = \dfrac{{R\sqrt 3 }}{2}\)
Xét tam giác vuông \(HOC\) có \(\sin \widehat {HOC} = \dfrac{{HC}}{{OC}} = \dfrac{{\sqrt 3 }}{2} \Rightarrow \widehat {HOC} = 60^\circ \Rightarrow \widehat {BOC} = 120^\circ \)
Độ dài cung nhỏ \(BC\) là \(l = \dfrac{{\pi .R.120}}{{180}} = \dfrac{{2\pi R}}{3}\) \(\left( {cm} \right)\) .
Hướng dẫn giải:
Bước 1: Tìm số đo cung bằng cách sử dụng tỉ số lượng giác của góc nhọn
Bước 2: Sử dụng công thức tính độ dài cung tròn:
Trên đường tròn bán kính$R$ , độ dài $l$ của một cung \(n^\circ \) được tính theo công thức \(l = \dfrac{{\pi Rn}}{{180}}\,\).
