Với giải Hoạt động khám phá 1 trang 7 Toán 11 Tập 1 Chân trời sáng tạo chi tiết trong Bài 1: Góc lượng giác giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:
Giải bài tập Toán lớp 11 Bài 1: Góc lượng giác
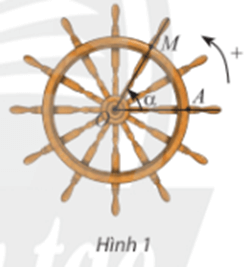
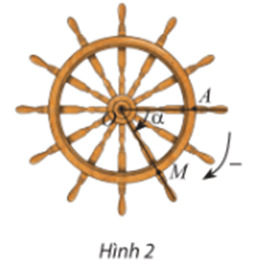
Hoạt động khám phá 1 trang 7 Toán 11 Tập 1: Một chiếc bánh lái tàu có thể quay theo cả hai chiều. Trong Hình 1 và Hình 2, lúc đầu thanh OM ở vị trí OA.
a) Khi quay bánh lái ngược chiều kim đồng hồ (Hình 1), cứ mỗi giây, bánh lái quay một góc 60°. Bảng dưới dây cho ta góc quay α của thanh OM sau t giây kể từ lúc bắt đầu quay. Thay dấu ? bằng số đo thích hợp.
|
Thời gian t (giây) |
1 |
2 |
3 |
4 |
5 |
6 |
|
Góc quay α |
60° |
120° |
? |
? |
? |
? |
b) Nếu bánh lái được quay theo chiều ngược lại, nghĩa là quay cùng chiều kim đồng hồ (Hình 2) với cùng tốc độ như trên, người ta ghi – 60° để chỉ góc mà thanh OM quay được sau mỗi giây. Bảng dưới đây cho ta góc quay α của thanh OM sau t giây kể từ lúc bắt đầu quay. Thay dấu ? bằng số đo thích hợp.
|
Thời gian t (giây) |
1 |
2 |
3 |
4 |
5 |
6 |
|
Góc quay α |
– 60° |
– 120° |
? |
? |
? |
? |
Lời giải:
a) Vì cứ mỗi giây, bánh lái quay một góc 60° nên tương ứng ta có:
Với t = 1 (giây) thì α = 60°;
Với t = 2 (giây) thì α = 2.60° = 120°;
Với t = 3 (giây) thì α = 3.60° = 180°;
Với t = 4 (giây) thì α = 4.60° = 240°;
Với t = 5 (giây) thì α = 5.60° = 300°;
Với t = 6 (giây) thì α = 6.60° = 360°;
Khi đó ta có bảng:
|
Thời gian t (giây) |
1 |
2 |
3 |
4 |
5 |
6 |
|
Góc quay α |
60° |
120° |
180° |
240° |
300° |
360° |
b) Vì cứ mỗi giây, bánh lái quay một góc – 60° nên tương ứng ta có:
Với t = 1 (giây) thì α = – 60°;
Với t = 2 (giây) thì α = 2.(– 60°) = – 120°;
Với t = 3 (giây) thì α = 3.(– 60°) = – 180°;
Với t = 4 (giây) thì α = 4.(– 60°) = – 240°;
Với t = 5 (giây) thì α = 5.(– 60°) = – 300°;
Với t = 6 (giây) thì α = 6.(– 60°) = – 360°;
Khi đó ta có bảng:
|
Thời gian t (giây) |
1 |
2 |
3 |
4 |
5 |
6 |
|
Góc quay α |
– 60° |
– 120° |
– 180° |
– 240° |
– 300° |
– 360 |