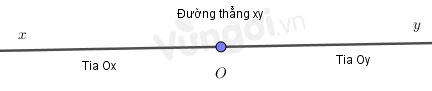
- Hình gồm điểm O và một phần đường thẳng bị chia ra bởi điểm O được gọi là một tia gốc O.
- Hai tia \(Ox\) và \(Oy\) là hai tia đối nhau.
Chú ý:
- Khi đọc (hay viết) tên một tia, phải đọc (hay viết) tên gốc trước.
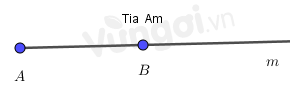
- Khi điểm \(B\) thuộc tia \(Am\) thì tia \(Am\) còn gọi là tia \(AB\)
- Mỗi điểm trên đường thẳng là gốc chung của hai tia đối nhau.
- Hai tia $Ox,Oy$ đối nhau. Nếu điểm $A$ thuộc tia $Ox$ và điểm $B$ thuộc tia $Oy$ thì điểm $O$ nằm giữa hai điểm $A$ và $B.$
- Hai tia trùng nhau có cùng gốc và có một điểm chung khác gốc.
Nghĩa là nếu điểm \(A\) thuộc tia \(Ox\,\left( {A \ne O} \right)\) thì hai tia \(Ox\) và \(OA\) trùng nhau.
Nhận xét:

- Nếu hai tia \(OA\) và \(OB\) đối nhau thì điểm \(O\) nằm giữa hai điểm \(A\) và \(B\)
- Ngược lại, nếu điểm \(O\) nằm giữa hai điểm \(A\) và \(B\) thì:
+ Hai tia \(OA;OB\) đối nhau
+ Hai tia \(AO;AB\) trùng nhau; hai tia \(BO;BA\) trùng nhau

