I. Hình chữ nhật
1. Nhận biết hình chữ nhật
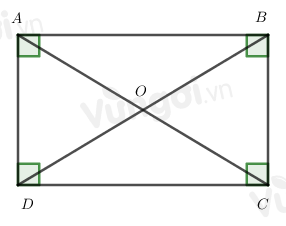
Hình chữ nhật ABCD có:
- Bốn đỉnh A, B, C, D
- Hai cặp cạnh đối diện bằng nhau: AB=CD;BC=AD.
- Hai cặp cạnh đối diện song song: AB song song với CD; BC song song với AD.
- Bốn góc ở đỉnh A, B, C, D bằng nhau và bằng góc vuông.
- Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường:
AC=BD và OA=OC;OB=OD.
2.Cách vẽ hình chữ nhật
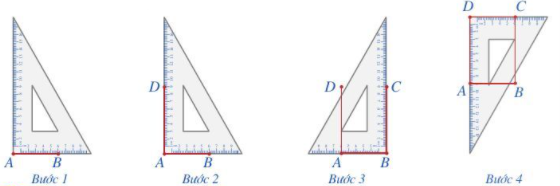
Bước 1. Vẽ theo một cạnh góc vuông của ê ke đoạn thẳng AB có độ dài bằng 6 cm
Bước 2. Đặt đỉnh góc vuông của ê ke trùng với điểm A và một cạnh ê ke nằm trên AB, vẽ theo cạnh kia của ê ke đoạn thẳng AD có độ dài bằng 9 cm
Bước 3. Xoay ê ke rồi thực hiện tương tự như ở Bước 2 để được cạnh BC có độ dài bằng 9 cm
Bước 4. Vẽ đoạn thẳng CD.
II. Chu vi và diện tích hình chữ nhật
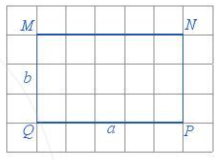
Chu vi của hình chữ nhật là: C=2(a+b);
Diện tích của hình chữ nhật là: S=a.b
Chú ý: Khi tính chu vi và diện tích thì chiều dài và chiều rộng phải cùng đơn vị đo.
Ví dụ 1:
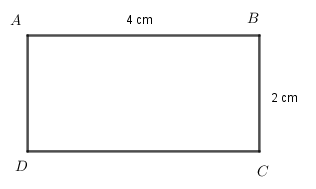
Chu vi hình chữ nhật ABCD là: 2.(4+2)=16(cm2).
Diện tích hình chữ nhật ABCD là: 4.2=8(cm2).
Ví dụ 2:
Bác Khôi muốn lát nền cho một căn phòng hình chữ nhật có chiều dài 8 m, chiều rộng 6 m. Loại gạch lát nền được sử dụng là gạch hình chữ nhật có chiều dài 20 cm, chiều rộng 50 cm. Hỏi bác Khôi phải sử dụng bao nhiêu viên gạch (coi mạch vữa không đáng kể)?
Giải:
Diện tích căn phòng hình chữ nhật là: 8.6=48(m2)
Diện tích của một viên gạch là: 20.50=1000(cm2)=0,1(m2)
Số viên gạch bác Khôi cần dùng là: 48:0,1=480 (viên).
III. Hình thoi
1. Nhận biết hình thoi
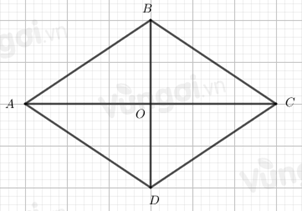
Hình thoi ABCD có:
- Bốn đỉnh A, B, C, D.
- Bốn cạnh bằng nhau: AB=BC=CD=DA;
- Hai cạnh đối AB và CD, AD và BC song song với nhau.
- Hai đường chéo AC và BD vuông góc với nhau.
- Vẽ hình thoi
Ví dụ: Dùng thước và compa vẽ hình thoi ABCD, biết AB=5cm và AC=8cm.
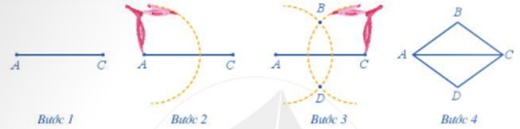
Bước 1. Dùng thước vẽ đoạn thẳng AC=8cm
Bước 2. Dùng compa vẽ một phần đường tròn tâm A bán kính 5cm.
Bước 3. Dùng compa vẽ một phần đường tròn tâm C bán kính 5cm; phần đường tròn này cắt phần đường tròn tấm A vẽ ở Bước 2 tại các điểm B và D.
Bước 4. Dùng thước vẽ các đoạn thẳng AB, BC, CD, DA.
IV. Chu vi và diện tích của hình thoi
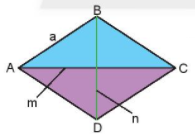
Chu vi hình thoi bằng độ dài cạnh nhân với bốn: C=4a
Diện tích hình thoi bằng nửa tích hai đường chéo: S=m.n2
Ví dụ 1:
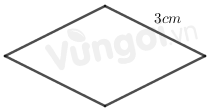
Chu vi hình thoi có cạnh bằng 3 cm là: 4.3=12(m2)
Ví dụ 2:
Hình thoi có độ dài hai đường chéo là 40 m và 20 m có diện tích là:
S=40.202=400(m2).

