I. Hình vuông
1.Nhận biết hình vuông
Bốn cạnh bằng nhau: \(AB = BC = CD = DA;\)
Hai cạnh đối \(AB\) và \(CD;\) \(AD\) và \(BC\) song song với nhau;
Hai đường chéo bằng nhau: \(AC = BD;\)
Bốn góc ở các đỉnh \(A,{\rm{ }}B,{\rm{ }}C,{\rm{ }}D\) là góc vuông.
2.Vẽ hình vuông
Ví dụ: Vẽ bằng ê ke hình vuông \(ABCD\), biết độ dài cạnh bằng \(7{\rm{ }}cm\).
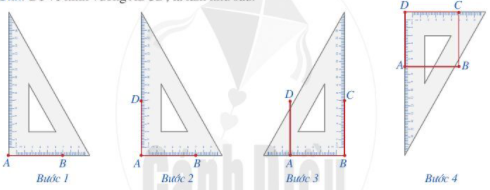
Bước 1. Vẽ theo một cạnh góc vuông của ê ke đoạn thẳng AB có độ dài bằng \(7{\rm{ }}cm\).
Bước 2. Đặt đỉnh góc vuông của ê ke trùng với điểm A và một cạnh ê ke nằm trên AB, vẽ theo cạnh kia của ê ke đoạn thẳng AD có độ dài bằng \(7{\rm{ }}cm\).
Bước 3. Xoay ê ke rồi thực hiện tương tự như ở Bước 2 để được cạnh BC có độ dài bằng \(7{\rm{ }}cm\).
Bước 4. Vẽ đoạn thẳng CD.
II. Thế nào là chu vi và diện tích
1. Chu vi
Chu vi của một hình bất kì là độ dài phần đường thẳng bao quanh hình đó.
Ví dụ:
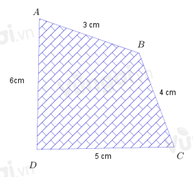
Chu vi của tứ giác ABCD bằng tổng độ dài bốn cạnh bao quanh nó, tức là:
\(AB + BC + CD + DA = 3 + 4 + 5 + 6 = 18\,\,(cm)\).
Chú ý: Khi tính chu vi các hình thì độ dài các cạnh phải cùng đơn vị đo.
2. Diện tích
Diện tích của một hình là toàn bộ phần bên trong của hình đó.
Ví dụ:
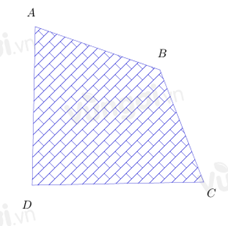
Diện tích của hình tứ giác trên là phần gạch xanh bên trong hình đó.
III. Chu vi và diện tích của hình vuông
Cho hình vuông có cạnh bằng \(a\):
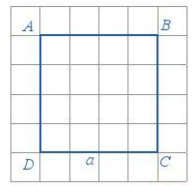
Chu vi hình vuông là: \(C = 4a\)
Diện tích hình vuông là: \(S = a.a = {a^2}\).
Ví dụ 1:
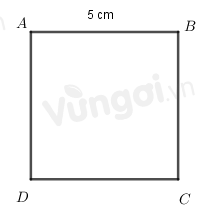
Chu vi hình vuông \(ABCD\) là: \(4.5 = 20\,(c{m^2})\)
Diện tích hình vuông \(ABCD\) là: \({5^2} = 25\,(c{m^2})\).
Ví dụ 2:
Một mảnh ruộng hình vuông có cạnh bằng \(15\,m\). Năng suất lúa là \(0,9\,kg/{m^2}\). Tính diện tích mảnh ruộng và sản lượng thu hoạch được.
Diện tích mảnh ruộng hình vuông là: \({15^2} = 225\,({m^2})\).
Sản lượng thu hoạch được là: \(225:0,9 = 312,5\)(kg).
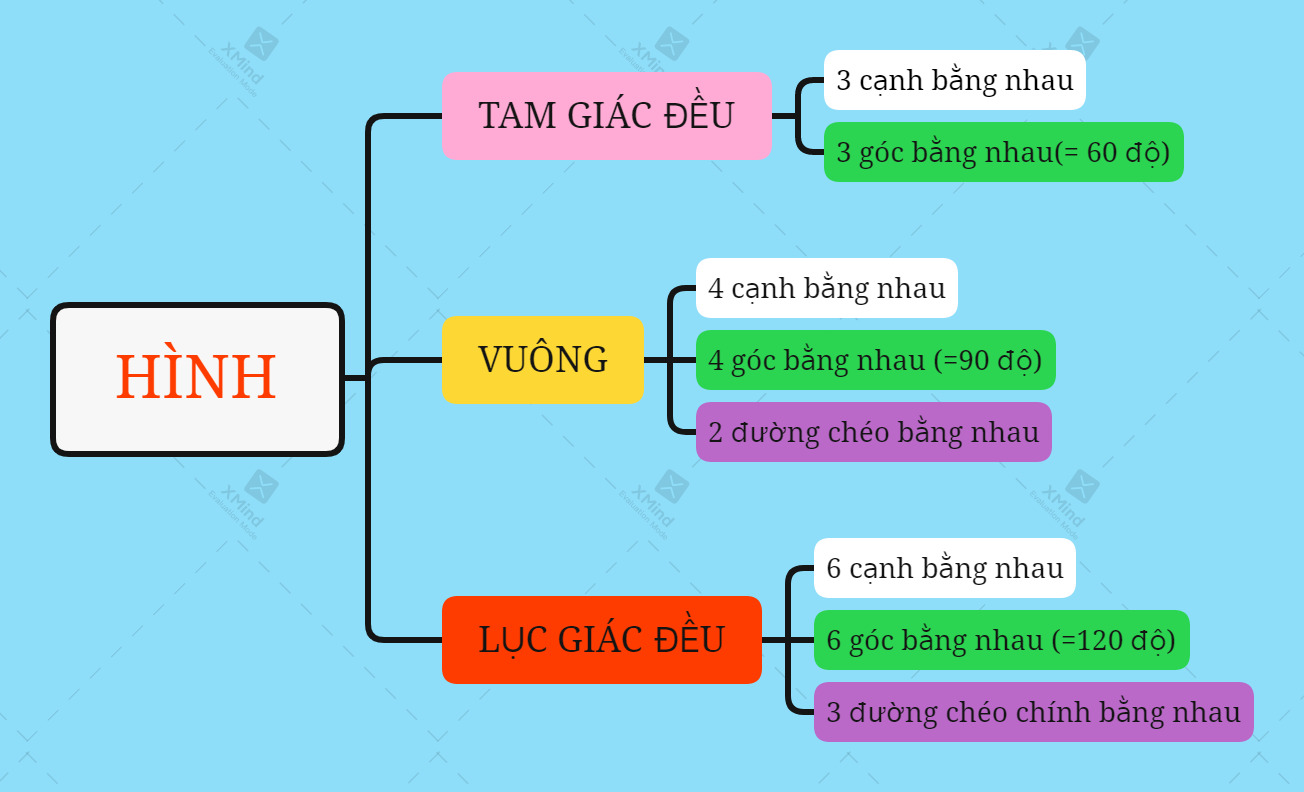
IV. Sơ đồ tư duy Hình vuông - Tam giác đều - Lục giác đều
