Câu hỏi:
2 năm trước
Từ \(A\) ở ngoài \(\left( O \right)\) vẽ tiếp tuyến \(AB\) và cát tuyến \(ACD\) . Tia phân giác \(\widehat {BAC}\) cắt \(BC,BD\) lần lượt tại \(M,N\) . Vẽ dây \(BF\) vuông góc với \(MN\) tại \(H\) và cắt \(CD\) tại \(E\) .
Tam giác \(BMN\) là tam giác gì?
Trả lời bởi giáo viên
Đáp án đúng: c
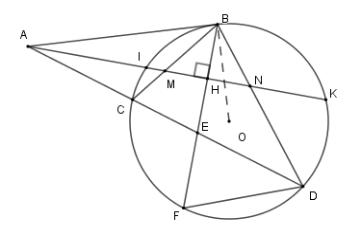
Xét \(\left( O \right)\) có đường thẳng \(AM\) cắt đường tròn tại \(I;K\) .
Khi đó
\(\widehat {BAK} = \dfrac{1}{2}\) (sđ \(\overparen{BK} - \) sđ \(\overparen{BI}\) );
\(\widehat {CAK} = \dfrac{1}{2}\) (sđ \(\overparen{DK} - \) sđ \(\overparen{CI}\) )
Mà \(\widehat {BAK} = \widehat {CAK} \)
\(\Rightarrow \) \(\dfrac{1}{2}\) (sđ \(\overparen{BK}- \) sđ \(\overparen{BI}\) )
\( = \dfrac{1}{2}\) (sđ \(\overparen{DK} - \) sđ \(\overparen{CI}\) )
Nên \( \dfrac{1}{2}\) (sđ \(\overparen{BK} + \) sđ \(\overparen{CI}\) )
\(=\dfrac{1}{2}\) (sđ \(\overparen{DK} + \) sđ \(\overparen{BI}\) )
Hay \(\widehat {BMN} = \widehat {BNM}\)
\(\Rightarrow \Delta BMN\) cân tại \(B\) .
Hướng dẫn giải:
Sử dụng góc có đỉnh bên trong đường tròn và góc có đỉnh bên ngoài đường tròn để chứng minh các góc bằng nhau
