Trong một thí nghiệm Y-âng về giao thoa ánh sáng, khoảng cách giữa hai khe là \(2mm\), khoảng cách từ hai khe đến màn quan sát là \(2m\). Nguồn sáng gồm hai bức xạ có bước sóng \({\lambda _1} = {\rm{ }}0,5{\rm{ }}\mu m\) và \({\lambda _2} = {\rm{ }}0,4{\rm{ }}\mu m\) . Trên bề rộng trường giao thoa \(L{\rm{ }} = {\rm{ }}13mm\), số vân sáng quan sát được là:
Trả lời bởi giáo viên
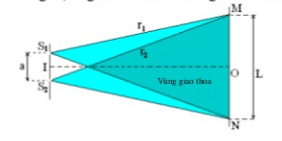
\({i_1} = \dfrac{{d{\lambda _1}}}{a} = 0,5mm,{i_2} = \dfrac{{d{\lambda _2}}}{a} = 0,4mm\)
\(\dfrac{{{k_2}}}{{{k_1}}} = \dfrac{{{\lambda _1}}}{{{\lambda _2}}} = \dfrac{5}{4}\)
\( \Rightarrow {i_{12}} = 4{i_1} = 2mm\)
Xét: \(\dfrac{L}{{2{i_1}}} = 13 \Rightarrow \) từ trung tâm tới M có 13 vân sáng của bức xạ 1 (không tính vân trung tâm)
\(\dfrac{L}{{2{i_2}}} = 16,25 \Rightarrow \) từ trung tâm tới M có 16 vân sáng của bức xạ 2 (không tính vân trung tâm)
\(\dfrac{L}{{2{i_{12}}}} = 3,25 \Rightarrow \) từ trung tâm tới M có 3 vân sáng trùng màu nhau (không tính vân trung tâm)
Suy ra từ trung tâm tới M có \(13 + 16 - 3 = 26\) vân sáng (không tính vân trung tâm)
Vậy trên màn có \(26.2 + 1 = 53\) vân sáng
Hướng dẫn giải:
+ Sử dụng lí thuyết về giao thoa đồng thời hai nguồn đơn sắc
+ Vị trí vân sáng \({x_s} = {\rm{ }}ki\)