Câu hỏi:
2 năm trước
Trong không gian với hệ trục tọa độ vuông góc \(Oxyz\), cho đường thẳng \(d:\dfrac{x}{1} = \dfrac{{y + 1}}{2} = \dfrac{{z - 2}}{{ - 1}}\) và mặt phẳng \(\left( P \right):x + y + z - 3 = 0\). Phương trình đường thẳng d' đối xứng với d qua (P) là
Trả lời bởi giáo viên
Đáp án đúng: b
Bước 1: Lấy điểm \(B\left( {0; - 1;2} \right)\) thuộc d.
Lấy điểm \(B\left( {0; - 1;2} \right)\) thuộc d.
Bước 2: Tìm giao điểm A của d và (P)
Gọi A là giao điểm của d và (P).
Khi đó \(A\left( {t; - 1 + 2t;2 - t} \right)\). Thay vào (P) ta được:
\(t - 1 + 2t + 2 - t - 3 = 0 \Leftrightarrow t = 1\)
=> \(A\left( {1;1;1} \right)\)
Bước 3: Tìm d’
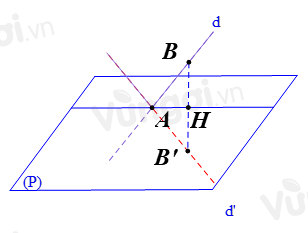
Gọi H là hình chiếu của B lên (P), B’ là điểm đối xứng B qua (P).
Khi đó H là trung điểm của BB’
Ta có đường thẳng BH đi qua B(0;-1;2) và nhận \(\overrightarrow {{n_{\left( P \right)}}} = \left( {1;1;1} \right)\) làm vecto chỉ phương có phương trình là:
\(\left\{ \begin{array}{l}x = t\\y = - 1 + t\\z = 2 + t\end{array} \right.\)
\( = > H\left( {t; - 1 + t;2 + t} \right)\). Thay vào (P) ta được:
\(t - 1 + t + 2 + t - 3 = 0 \Leftrightarrow t = \dfrac{2}{3}\)
\( = > H\left( {\dfrac{2}{3}; - \dfrac{1}{3};\dfrac{8}{3}} \right)\)\( = > B'\left( {\dfrac{4}{3};\dfrac{1}{3};\dfrac{{10}}{3}} \right)\)
Vecto chỉ phương của AB’ là:
\(AB' = \left( {\dfrac{1}{3}; - \dfrac{2}{3};\dfrac{7}{3}} \right)\)
Đường thẳng \(d':\dfrac{{x - 1}}{1} = \dfrac{{y - 1}}{{ - 2}} = \dfrac{{z - 1}}{7}\)
Hướng dẫn giải:
Bước 1: Lấy điểm \(B\left( {0; - 1;2} \right)\) thuộc d.
Bước 2: Tìm giao điểm A của d và (P)
Bước 3: Gọi H là hình chiếu của B lên (P), B’ là điểm đối xứng B qua (P). Tìm d’
