Câu hỏi:
2 năm trước
Trong không gian với hệ tọa độ Oxyz cho H (2; 1; 1). Gọi (P) là mặt phẳng đi qua H và cắt các trục tọa độ tại A; B; C sao cho H là trực tâm tam giác ABC. Phương trình mặt phẳng (P) là:
Trả lời bởi giáo viên
Đáp án đúng: a
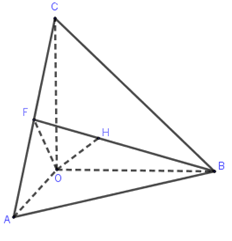
Gọi \(BH \cap AC = \left\{ F \right\} \Rightarrow BF \bot AC\).
Lại có \(BO \bot \left( {OAC} \right)\) nên \(BO \bot AC\).
Do đó \(AC \bot \left( {BOF} \right) \Rightarrow AC \bot OH\).
Chứng minh tương tự ta được \(BC \bot OH \Rightarrow OH \bot \left( {ABC} \right)\).
Do đó mặt phẳng \(\left( P \right)\) đi qua \(H\left( {2;1;1} \right)\) và có véc tơ pháp tuyến \(\overrightarrow n = \overrightarrow {OH} = \left( {2;1;1} \right)\) nên \(\left( P \right)\) có phương trình:
\(2\left( {x - 2} \right) + 1\left( {y - 1} \right) + 1\left( {z - 1} \right) = 0 \Leftrightarrow 2x + y + z - 6 = 0\)
Vậy \(\left( P \right):2x + y + z - 6 = 0\).
Hướng dẫn giải:
- Chứng minh \(\overrightarrow {OH} \bot \left( P \right)\) bằng cách sử dụng định lý: “Đường thẳng vuông góc với hai đường thẳng cắt nhau thì nó vuông góc với mặt phẳng chứa hai đường thẳng đó”.
- Viết phương trình \(\left( P \right)\) đi qua điểm \(H\) và có véc tơ pháp tuyến \(\overrightarrow {OH} \):
Phương trình mặt phẳng đi qua điểm \(M\left( {{x_0};{y_0};{z_0}} \right)\) và có véc tơ pháp tuyến \(\overrightarrow n = \left( {a;b;c} \right)\) là:
\(a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) + c\left( {z - {z_0}} \right) = 0\).
