Câu hỏi:
2 năm trước
Gọi \(\left( P \right)\) là mặt phẳng chứa điểm \(B\left( {0;1;2} \right)\) sao cho khoảng cách từ điểm \(A\left( {1;2;1} \right)\) đến \(\left( P \right)\) là lớn nhất. Phương trình của \(\left( P \right)\) là:
Trả lời bởi giáo viên
Đáp án đúng: b
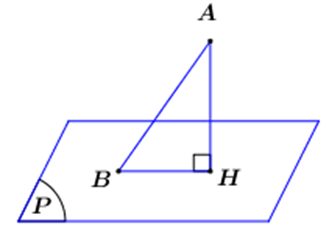
Gọi \(H\) là hình chiếu vuông góc của \(A\) lên \(\left( P \right)\), khi đó ta có \(AH \le AB\) (quan hệ giữa đường vuông góc và đường xiên).
Do đó \(d{\left( {A;\left( P \right)} \right)_{\max }} \Leftrightarrow A{H_{\max }} \Leftrightarrow H \equiv B\), khi đó \(AB \bot \left( P \right)\).
Khi đó \(\left( P \right)\) nhận \(\overrightarrow {AB} = \left( {1;1; - 1} \right)\) là 1 vtpt.
Vậy để khoảng cách từ điểm \(A\left( {1;2;1} \right)\) đến \(\left( P \right)\) là lớn nhất thì phương trình của \(\left( P \right)\) là:
\(1\left( {x - 0} \right) + 1\left( {y - 1} \right) - 1\left( {z - 2} \right) = 0\) \( \Leftrightarrow x + y - z + 1 = 0\).
Hướng dẫn giải:
- Gọi \(H\) là hình chiếu vuông góc của \(A\) lên \(\left( P \right)\), chứng minh \(AH \le AB\).
- Viết phương trình mặt phẳng \(\left( P \right)\) khi \(A{H_{\max }} = AB\).
- Phương trình mặt phẳng đi qua \(M\left( {{x_0};{y_0};{z_0}} \right)\) và có 1 VTPT \(\overrightarrow n \left( {A;B;C} \right)\) là:
\(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) \)\(0\)
