Câu hỏi:
2 năm trước
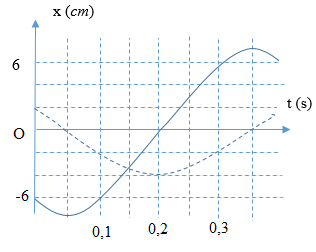
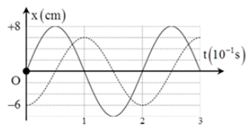
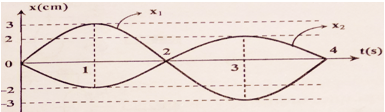
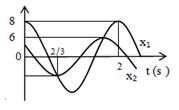
Trên trục x có hai vật tham gia hai dao động điều hoà cùng tần số với các li độ \({x_1}\) và \({x_2}\) có đồ thị biến thiên theo thời gian như hình sau.Vận tốc tương đối giữa hai vật có giá trị cực đại gần nhất với các giá trị nào sau đây?
Trả lời bởi giáo viên
Đáp án đúng: d
Từ đồ thị ta có: \(\left\{ \begin{array}{l}{x_1} = 8\cos (\pi t)(cm)\\{x_2} = 6.cos\left( {\pi t + \dfrac{\pi }{3}} \right)cm\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{v_1} = - 8\pi \sin \pi t\,\,\,(cm/s)\\{v_2} = - 6\pi .sin\left( {\pi t + \dfrac{\pi }{3}} \right)\,\,(cm/s)\end{array} \right.\)
Vận tốc tương đối của vật 1 đối với vật 2 : \({v_{12}} = {\rm{ }}{v_1}-{\rm{ }}{v_2}\)
Dùng vectơ quay ta có :
\(v_{12max}^2 = v_1^2 + v_2^2 - 2{v_1}.{v_2}.\cos \dfrac{\pi }{3} = {\left( {8\pi } \right)^2} + {\left( {6\pi } \right)^2} - 2.{8\pi}.{6\pi}\cos \dfrac{\pi }{3} \Rightarrow {v_{12max}} = 2\pi \sqrt {13} \,(cm/s) \approx 22,65\left( {cm/s} \right)\)
Hướng dẫn giải:
+ Viết phương trình vận tốc từ phương trình li độ: \(x = A\cos \left( {\omega t + \varphi } \right) \to v = - A\omega \sin \left( {\omega t + \varphi } \right)\)
+ Sử dụng véc-tơ quay
Câu hỏi khác
- Bài tập lí thuyết dao động điều hòa có lời giải MÔN LÝ lớp 12
- Bài tập xác định thời gian vật chuyển động từ x1 đến x2, số lần qua li độ x có lời giải MÔN LÝ lớp 12
- Bài tập các đại lượng đặc trưng của DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập xác định quãng đường, tốc độ trung bình của vật trong DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập viết phương trình dao động điều hòa có lời giải MÔN LÝ lớp 12
